and are given points. D (11, 9) is the mid point of AB and E (41, 39) is the mid point of BC. If F is the mid point of AC then is equal to , where K =
The correct Answer is:
To solve the problem, we need to find the value of K such that (BF)2=K2. We will follow these steps:
Step 1: Find the coordinates of points A, B, and C
Given:
- A(a+1,a−1)
- B(a2+1,a2−1)
- C(a3+1,a3−1)
Step 2: Use the midpoint formula to find D
The midpoint D of points A and B is given by:
D=((a+1)+(a2+1)2,(a−1)+(a2−1)2)
This simplifies to:
D=(a+a2+22,a+a2−22)
Step 3: Set the coordinates of D equal to (11, 9)
Since D(11,9):
a+a2+22=11anda+a2−22=9
From the first equation:
a+a2+2=22⟹a2+a−20=0
From the second equation:
a+a2−2=18⟹a2+a−20=0
Both equations are the same.
Step 4: Solve the quadratic equation
The quadratic equation a2+a−20=0 can be factored:
(a−4)(a+5)=0
Thus, a=4 or a=−5.
Step 5: Find the coordinates of B and C for both values of a
1. For a=4:
- B(42+1,42−1)=B(17,15)
- C(43+1,43−1)=C(65,63)
2. For a=−5:
- B((−5)2+1,(−5)2−1)=B(26,24)
- C((−5)3+1,(−5)3−1)=C(−124,−126)
Step 6: Find the midpoint E of BC
Using the midpoint formula for B and C:
E=(xB+xC2,yB+yC2)
1. For a=4:
E=(17+652,15+632)=(41,39)
2. For a=−5:
E=(26−1242,24−1262)=(−49,−51)
Step 7: Find the midpoint F of AC
Using the midpoint formula for A and C:
F=(xA+xC2,yA+yC2)
1. For a=4:
F=(5+652,3+632)=(35,33)
2. For a=−5:
F=(−4−1242,−6−1262)=(−64,−66)
Step 8: Calculate (BF)2
Using the distance formula:
(BF)2=(xB−xF)2+(yB−yF)2
1. For a=4:
(BF)2=(17−35)2+(15−33)2=(−18)2+(−18)2=324+324=648
2. For a=−5:
(BF)2=(26+64)2+(24+66)2=(90)2+(90)2=8100+8100=16200
Step 9: Find K
From the calculations:
1. For a=4:
K2=648⟹K=√648=18√2
2. For a=−5:
K2=16200⟹K=√16200=90√2
Final Answer
The value of K for a=4 is 18√2 and for a=−5 is 90√2.
Given:
- A(a+1,a−1)
- B(a2+1,a2−1)
- C(a3+1,a3−1)
The midpoint D of points A and B is given by:
D=((a+1)+(a2+1)2,(a−1)+(a2−1)2)
This simplifies to:
D=(a+a2+22,a+a2−22)
Since D(11,9):
a+a2+22=11anda+a2−22=9
From the first equation:
a+a2+2=22⟹a2+a−20=0
From the second equation:
a+a2−2=18⟹a2+a−20=0
Both equations are the same.
The quadratic equation a2+a−20=0 can be factored:
(a−4)(a+5)=0
Thus, a=4 or a=−5.
1. For a=4:
- B(42+1,42−1)=B(17,15)
- C(43+1,43−1)=C(65,63)
- B((−5)2+1,(−5)2−1)=B(26,24)
- C((−5)3+1,(−5)3−1)=C(−124,−126)
Using the midpoint formula for B and C:
E=(xB+xC2,yB+yC2)
1. For a=4:
E=(17+652,15+632)=(41,39)
E=(26−1242,24−1262)=(−49,−51)
Using the midpoint formula for A and C:
F=(xA+xC2,yA+yC2)
1. For a=4:
F=(5+652,3+632)=(35,33)
F=(−4−1242,−6−1262)=(−64,−66)
Using the distance formula:
(BF)2=(xB−xF)2+(yB−yF)2
1. For a=4:
(BF)2=(17−35)2+(15−33)2=(−18)2+(−18)2=324+324=648
(BF)2=(26+64)2+(24+66)2=(90)2+(90)2=8100+8100=16200
From the calculations:
1. For a=4:
K2=648⟹K=√648=18√2
K2=16200⟹K=√16200=90√2
The value of K for a=4 is 18√2 and for a=−5 is 90√2.
Topper's Solved these Questions
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (CONCEPT - BASED) SINGLE CORRECT ANSWER TYPE QUESTIONS
15 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - EXERCISE (LEVEL 1) SINGLE CORRECT ANSWER TYPE QUESTIONS
60 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - SOLVED EXAMPLES (LEVEL 2) SINGLE CORRECT ANSWER TYPE QUESTIONS
30 Videos
- AREA BY INTEGRATIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - AREA BY INTEGRATIONEXERCISE - Question from Previous Years. B-Architecture Entrance Examination Papers
12 Videos
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
17 Videos
Similar Questions
Knowledge Check
In a ΔABC,D is the mid - point of BC and E is mid - point of AD, BF passes through E. What is the ratio of AF:FC?
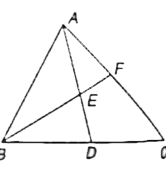 A1:1B1:2C1:3D2:3
A1:1B1:2C1:3D2:3In figure given below ∠B=70∘,∠C=60∘,E is the mid point of BC, F is the mid point of AB, then the value of ∠FEB is
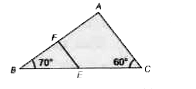 A40∘B60∘C70∘D50∘
A40∘B60∘C70∘D50∘
D is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIn ΔABC,D is the mid-pointpoint of BC and E is mid-point of AD.BE is produced to meet the side AC in F.Then BF is equal to
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC
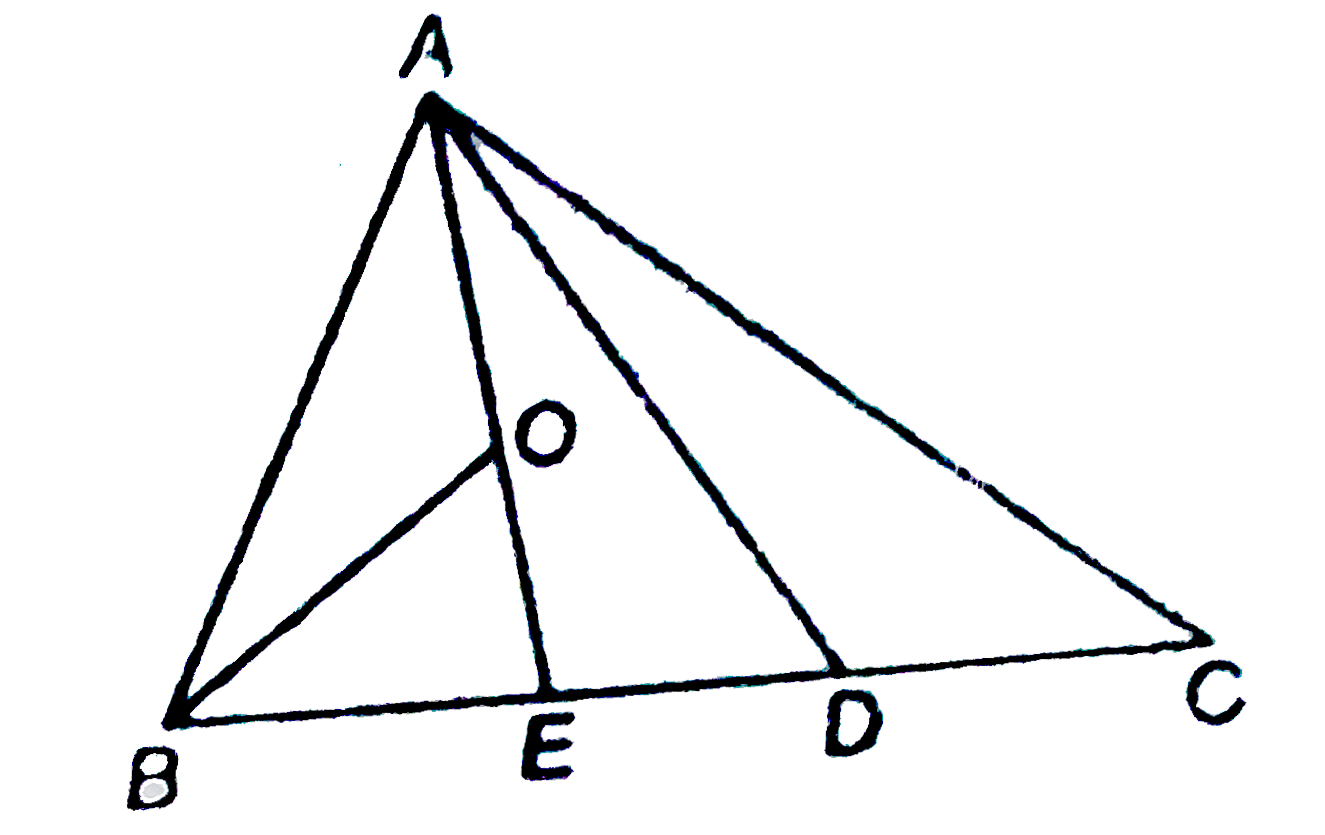
View SolutionA(a,b) and B(0,0) are two fixed points. If M1 is the mid point of ¯¯¯¯¯¯AB,M2 is mid point of ¯¯¯¯¯¯¯¯AM1,M3 is mid point of ¯¯¯¯¯¯¯¯AM2 and so on then M5 is
View SolutionIf D, E and F are respectively, the mid-points of AB, AC and BC in ΔABC, then BE + AF is equal to
View Solution
