A lamppost stands in the centre of a circular garden and makes angle α at point A and B on the boundary where AB subtends an angle 2β at the foot of the lamppost. If γ is the angle which the lamppost subtends at C, the middle point of the line joining A and B, then tanγ =
tanαtanβ
secαtanβ
tanαsecβ
None of these
The correct Answer is:C
Topper's Solved these Questions
- HEIGHTS AND DISTANCES BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEIGHTS AND DISTANCES EXERCISE - EXERCISE (NUMERICAL ANSWER TYPE QUESTIONS )
5 Videos
- HEIGHTS AND DISTANCES BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEIGHTS AND DISTANCES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. AIEEE/JEE MAIN PAPERS
20 Videos
- HEIGHTS AND DISTANCES BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEIGHTS AND DISTANCES EXERCISE - EXERCISE (LEVEL-1 ( SINGLE CORRECT ANSWER TYPE QUESTIONS ))
25 Videos
- ELLIPSEBOOK - MCGROW HILL PUBLICATIONCHAPTER - ELLIPSEEXERCISE - Previous Years B-Architecture Entrance Examination Papers
6 Videos
- HYPERBOLABOOK - MCGROW HILL PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - QUESTION FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
8 Videos
Similar Questions
A tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30∘ . The height of the tower is (1) 2a√3 (2) 2a√3 (3) a√3 (4) a√3
View Solution
Knowledge Check
A pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point B on the boundary. If the chord AB subtends an angle α at the centre of the path, the height of the pole is
A2acos(α/2)tanαB2asin(α/2)cotαC2asin(α/2)tanαD2acos(α/2)cotαA lamp post standing at a point A on a circular path of radius r subtends an angle α at some point B on the path, and AB subtends an angle of 45∘ at any other point on the path, then height of the lampost is
A√2rcotαB(r/√2)tanαC√2rtanαD(r/√2)cotαA vertical pole stands at a point A on the boundary of a circular park of radius a and subtends an angle α at another point β on the boundary. If the chord AB subtends an angle α at the centre of the park, the height of the pole is
A2a sinα2tanαB2a cosα2tanαC2a sinα2cotαD2a cosα2cotα
A tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
View SolutionA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60∘ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30∘. The height of the tower is
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB(=alpha) subtends an angle of elevation of the top of the first tower from A or B is 30∘. The height of the tower is
View SolutionA vertical pole stands at a point A on the boundary of a circular park of radius 2 km and subtends an angle 60∘ at another point B on the boundary. If the chord AB subtends the same angle 60∘ at the centre of the park, the height of the pole is
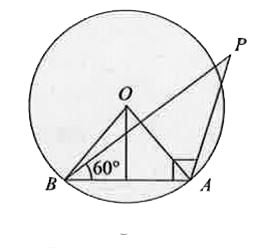
View SolutionThree poles of height a, b, c stand on the same side of a road and subtend an angle of 45∘ at a point on the line joining their feet. The pole of height a subtends an angle α at the foot of the pole of height b which subtends an angle β at the foot of the pole with height c, if a>b>c, then cotα−cotβ =
View Solution
