The co-ordinates of the vertices are A(x1,y1), B(x2,y2) and C(x3,y3). The line joining the points A and B is divided by a point P in the ratio l:k and line joining P and C is divided by point Q in the ratio m:k+l.Find co-ordinates of Q.
Step by step video & image solution for The co-ordinates of the vertices are A(x1,y1), B(x2,y2) and C(x3,y3). The line joining the points A and B is divided by a point P in the ratio l:k and line joining P and C is divided by point Q in the ratio m:k+l.Find co-ordinates of Q. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
The co-ordinates of the vertices are A(x1,y1), B(x2,y2) and C(x3,y3). The line joining the points A and B is divided by a point P in the ratio l:k and line joining P and C is divided by point Q in the ratio m:k+l.Find co-ordinates of Q.
View SolutionThe line segment joining the points (1,2) and (k,1) is divided by the line 3x + 4y -7=0in the ratio 4:9 then k is
View Solution
Knowledge Check
The line segment joining the points A(3,2) and B (5,1) is divided at the point P in the ratio 1:2 and it lies on the line 3x−18y+k=0. Find the value of k.
A19B18C17D16If point P (1,1) divides line segment joining the points A and B (-1,-1) in the ratio 5:2 , then co-ordinates of A are
A(3,3)B(6,6)C(2,2)D(1,1)
The line segment joining the points A(3,2) and B (5,1) is divided at the point P in the ratio 1:2 and it lies on the line 3x−18y+k=0. Find the value of k.
View SolutionIf the point P (−1,2) divides the line segment joining A (2,5) and B in the ratio 3:4 , find the co-ordinate of B .
View SolutionIf the point P (−1,2) divides the line segment joining A (2,5) and B in the ratio 3:4 , find the co-ordinate of B .
View SolutionThe line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x - y + k = 0, find the value of k. Also, find the co-ordinates of point Q.
View SolutionThe line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that PBAB=15. Find the co-ordinates of P.
View SolutionM is the mid-point of the line segment joining the points A(0, 4) and B(6, 0). M also divides the line segment OP in the ratio 1:3. Find :
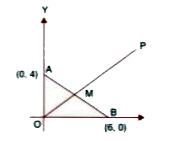
co-ordinates of P
View Solution
