For the reaction N2O5→2NO2+12O2, Given −d[N2O5]dt=K1[N2O5],d[NO2]dt=K2[N2O5] and d[O2]dt=K3[N2O4]. The relation in between K1,K2 and K3 is Solution in Telugu
2K1=K2=4K3
K1=K2=K3
2K1=4K2=K3
None of these
The correct Answer is:A
K11=K22=K3(1/2)=K11=K22=2.K3⇒2K1=K2=4K3
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - PRACTICE SHEET-1 (LINKED COMPREHENSION TYPE QUESTIONS)6videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - PRACTICE SHEET-1 (MATCH THE FOLLOWING QUESTIONS)2videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-II(LECTURE SHEET EXERCISE-IV INTEGER ANSWER TYPE QUESTIONS)10videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETCSEXERCISE - EXERCISE - 3.245videos
CHEMICAL KINETCS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - Additional Practice Exercise54videos
CHEMICAL THERMODYNAMICS
Similar Questions
The instantaneous rate of an elementary chamical reactkon aA+bB⇔cC+dD can be given by rate =Kf[A]a[B]b−Kb[C]c[D]d where Kf and Kb are rate constants for forward and backward reactions respectively for the reversible reaction. If the reaction is an irreversible one, the rate is expressed as, rate =K[A]a[B]b where K is rate contant for the given irreversible rate of disappearance of A is a/b times the rate of disappearance of B. The variation of rate constant K with temperature is expressed in terms of Arrhenius equation: K=Ae−Ea/RT whereas the ratio KfKb is expressed in terms of van't Hoff isochore: KfKb=Ae−ΔH/RT, where Ea and ΔH are energy of activation and heat of reaction respectively.
The variation of rate constant K and KfKb with temperature shows the following effects:
For endothrmic reaction when T increases then K increases and KfKb also increases.
(ii) For endothemic reaction when T decreases then K decreases and KfKb also decreases.
(iii) For exothermic when T increases then K and KfKb both increases.
(iv) For exothermic reaction when T decreases then K increases and KfKb decrease.
(v) For exothermic reaction when T increases thenK and KfKb both decrease.04:20View SolutionMatch the following columns
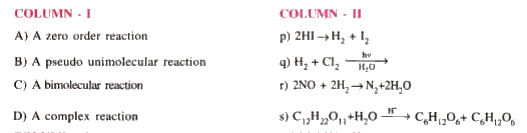 02:14View Solution
02:14View SolutionFor the reaction A→ products the following dats is given for a particular run
time (in): 0 5 15 35
1[A](M−1):1 2 4 8
Determine the order of the reaction.03:00View SolutionDiscuss on the kinetic spontaneity of a chemical reaction. Is a slow reaction spontaneous? Why?
02:23View SolutionWhich among the following is not an exact differential?
03:04View SolutionWhen N_(2)O_(5)(g) is heated it dissociates to give N_(2)O_(3) and O_(2) . K_(c) for N_(2)O_(5)rarr N_(2)O_(3)+O_(2) is 7.75 and K_(c) for N_(2)O_(3)rarr N_(2)O+O_(2) is 4.0 mol L^(-1) . (both K_(c) are at same temperature) 4 mol N_(2)O_(5) in 1.0L vessel is kept at a certain temperature. the concentration of O_(2) was 4.5 mol L^(-1) . Find the concentration of N_(2)O_(5), N_(2)O_(3) , and N_(2)O at equilibrium.
03:04View Solution2N2O5→4NO2+O2
If −d[N2O5]dt=k1[N2O5]
d[NO2]dt=k2[N2O5]
d[O2]dt=k3[N2O5]
What is the relation between k1,k2, and k3?04:45View SolutionFor the reaction,
N2O5→2NO2+12O2,Given
−d[N2O5]dt=K1[NO2O5]
d[NO2]dt=K2[N2O5]andd[O2]dt=K3[N2O5]
The relation in between K1,K2 and K3 is:05:16View SolutionConsider the following reaction, 2N_(2)O_(5)rarr4NO_(2)+O_(2),(d[NO_(2)] )/(dt)=k_(2)[N_(2)O_(5)] , (d[O_(2)])/(dt)=k_(3)[N_(2)O_(5)]" and "(d)/(dt)[N_(2)O_(5)]=k_(1) The relation between k_(1), k_(2) and k_(3) is
03:34View SolutionConsider the decomposition of N2O5 as
N2O5→2NO2+1/2O2
The rate of reaction is given by
−d[N2O5]dt=12d[NO2]dt=2d[O2]dt
=k1[N2O5]
Therefore −d[N2O5]dt=k1[N2O5]
+d[NO2]dt=2k1[N2O5]=k1[N2O5]
+d[O2]dt=12k1[N2O5]=k1[N2O5]
Choose the correct option03:01View SolutionConsider the decomposition of N2O5 as
N2O5→2NO2+1/2O2
The rate of reaction is given by
−d[N2O5]dt=12d[NO2]dt=2d[O2]dt
=k1[N2O5]
Therefore −d[N2O5]dt=k1[N2O5]
+d[NO2]dt=2k1[N2O5]=k1[N2O5]
+d[O2]dt=12k1[N2O5]=k1[N2O5]
Choose the correct option03:59View Solution2N_(2)O_(5)rarr NO_(2)+O_(2), (d[N_(2)O_(5)])/(dt)=k_(1)[N_(2)O_(5)], (d[NO_(2)])/(dt)=k_(2)[N_(2)O_(5)] and (dO_(2))/(dt)=k_(3)[N_(2)O_(5)] , the relation between k_(1), k_(2) and k_(3) is
01:53View SolutionConsider the reaction 2N2O5(g)→4NO2(g)+O2(g) whose rate can be expressed any one of the following expressions (1)−d[N2O5]dt=k1[N2O5] or (2)d[NO2]dt=k2[N2O5] or (3)d[O2]dt=k3[N2O5]
Find the relation between k1,k2andk3 .04:17View Solution2N2O5→4NO2+O2,d[N2O5]dt=k1[N2O5].
d[NO2]dt=k2[N2O5]andd[O2]dt=k3[N2O5], the relation between k1,k2andk3 is02:30View SolutionN2O2⇔2NO,K1,12N2+12O2⇔NO.K2,2NO⇔N2+O2.K3,NO⇔12N2+12O2.K4
02:26View Solution

