By using intergration prove that the area of a circle of radius r units is $π r^{2}$ square units.

Video Solution

Text Solution

Verified by Experts

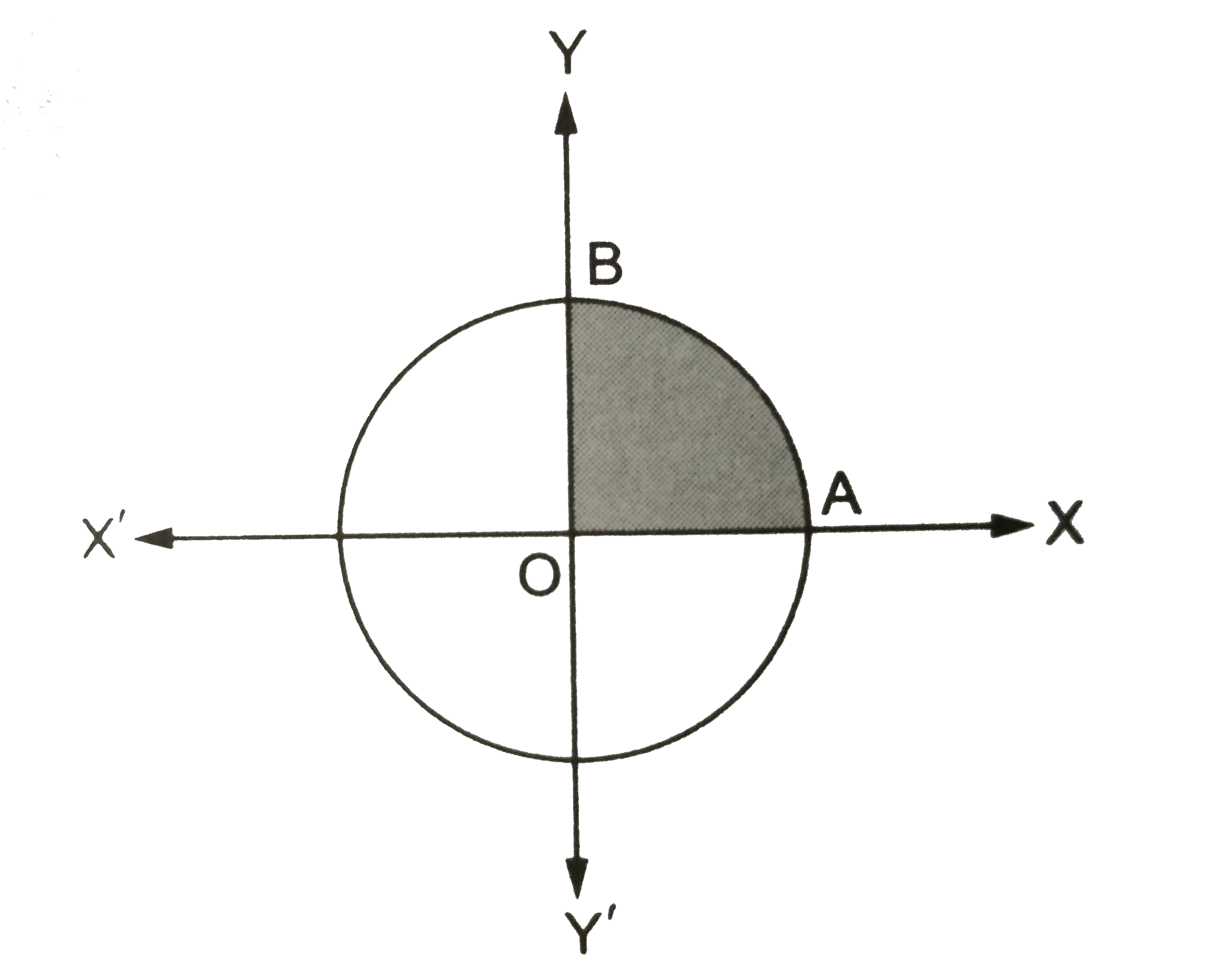
The equations of a circle of radius r units with its centre at the origin is
$x^{2} + y^{2} = r^{2} \dots (i)$
This equation contaions only even powers of y.
So the curve is symmetrical about the x-axis .Also the above equation contains only even powers of x . So the curve is symmetrical about the y- axies
Now $x^{2} + y^{2} = r^{2} \Rightarrow y = \sqrt{r^{2} - x^{2}}$
Area of the circle $= 4 \times$ (area OABO)
$= 4 \times r \int 0 y d x = 4 \times r \int 0 \sqrt{r^{2} - x^{2}} d x$
$= 4 \times π / 2 \int 0 r^{2} {cos}^{2} θ d θ$ ["putting"x=r sin $θ$ ]
$= 4 r^{2} . π / 2 \int 0 \frac{(1 + cos 2 θ)}{2} d θ = 2 r^{2} . {[θ + \frac{sin 2 θ}{2}]}_{0}^{π / 2}$
$(π r^{2})$ sq units
Hence , the required area is $(π r^{2})$ sq units

Updated on:21/07/2023

The area of a square made in a circle of radius r is
A $π r^{2}$
B $3 r^{2}$
C $2 r^{2}$
D $4 r^{2}$
Using the definite integration area of the circle with radius 4 unit is______
A $5 π$ sq . Untis
B4sq. Units
C16 sq. units
D $16 π s q .$ units
The radius of base and curved surface area of a right cylinder is 'r' units and $4 π r h$ square units respectively. The height of the cylinder is :
A $\frac{h}{2}$ units
Bh units
C2 h units
D4 h units