Let there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ(54−rR) upto r=R, and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at a distance r(rltR) from the origin is given by
ρ0r3ε0(54−rR)
4πρ0r3ε0(53−rR)
ρ0r4ε0(53−rR)
4ρ0r3ε0(54−rR)
The correct Answer is:C
Consider a thin spherical shell of radius x and thickness dx as shown in the figure.
Volume of the shell, dV=4πx2dx
Let us draw a Gaussian surface of radius r(r<R) as shown in the figure. Total charge enclosed inside the Gaussian surface is
Qin=r∫0ρdV=r∫0ρ0(54−xR)4πx2dx=4πρ0r∫0(54x2−x3R)dx
=4πρ0[512x3−x44R]r0=4πρ0[512r3−r44R]
=4πρ04[53r3−r4R]=πρ0[53r3−r4R]
According to Gauss.s law,
E4πr2=Qinε0⇒E4πr2=πρ0ε0[53r3−r4R]
E=πρ0r34πr2ε0[53−rR],E=ρ0r4ε0[53−rR]

Topper's Solved these Questions
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET ITALS
1 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET VITALS
18 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- ELECTRONIC DEVICESBOOK - MTG GUIDECHAPTER - ELECTRONIC DEVICESEXERCISE - AIPMT/NEET (MCQs)
42 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
[" Consider a spherical symmetric "],[" charge distribution with charge "],[" density varying as "],[[rho={[rho_(0)(1-(r)/(R)),r<=R],[0],r>R]]
View SolutionConsider a spherical symmetric charge distribution with charge density varying as ρ={[ρ0(1−rR),r≤R][0,,r>R]}The electric field at r ,r≤R will be
View Solution
Knowledge Check
Let there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
Aρ0r24ε0RBρ0r4ε0RCρ0r4ε0RDρ0r2ε0RA spherical distribution of charge density ρ=ρ0(1−r2/9) exists in the region 0≤r≤2. The dielectric constant of the medium is 2. Find the electric field inside the sphere at a distance r from the centre.
Aρ090ε0[15r−r3]Bρ045ε0[5r−8r3]Cρ05ε0[45r−2r3]Dρ02ε0[3r−4r3]The mass density of a spherical body is given by ρ(r)=kr for r≤R and ρ(r)=0for r > R , where r is the distance from the centre. The correct graph that describes qualitatively the acceleration, a, of a test particle as a function of r is :
A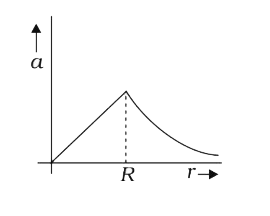 B
B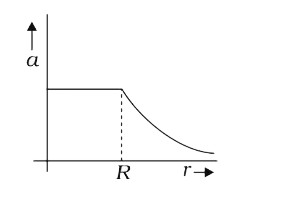 C
C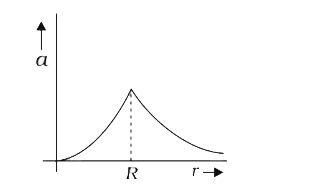 D
D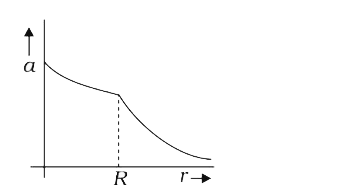
A point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionFor a spherically symmetrical charge distribution electric field at a distance r from the centre of sphere is →E=kr2ˆr where k is a constant what will be the volume charge density at a distance r from the centre of sphere?
View SolutionIn a spherical distribution , the charge density varies as ρ(r)=A/r for a<r<b (as shown) where A is constant . A point charge Q lies at the centre of the sphere at r = 0 . The electric filed in the region a<r<b has a constant magnitude for
View SolutionFor spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is →E=kr7→r, where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?
View Solution
