The capacities of three capacitors are in the ratio of 1:2:3. Their equivalent capacity in parallel is greater than their equivalent capacity in series by 60/11 pF. Calculate their individual capacitance.
4,6,7
1,2,3
2,3,4
1,3,6
The correct Answer is:B
Let, C1=C0,C2=2C0,C3=3C0
Their equivalent capacity, when they are connected in parallel
CP=C1+C2+C3=6C0
Their equivalent capacity, when they are connected in series
(1CS)=1C0[11+12+13]∴CS=6C011
∴CP−CS=6011C0
Given : Cp−CS=6011
From (i) and (ii), we get
60C011=6011 or C0=1
Hence, C1=1μF,C2=2μF,C3=3μF
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET ITALS1videos
ELECTROSTATICS
- BOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET VITALS18videos
ELECTROSTATICS
- BOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)34videos
ELECTROSTATICS
- BOOK - MTG GUIDECHAPTER - ELECTRONIC DEVICESEXERCISE - AIPMT/NEET (MCQs)42videos
ELECTRONIC DEVICES
- BOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)48videos
MAGNETIC EFFECTS OF CURRENT AND MAGNETISM
Similar Questions
The capacities of three capacitors are in the ratio of 1:2:3. Their equivalent capacity in series is greater than their equivalent capacity in series by 60/11 pF. Calculate their individual capacitances.
View SolutionThree capacitors each of capacitor 2μF are connected in series. Find resultance capacity in farad.
View Solution
Knowledge Check
- Question 1 - Select One
The equivalent capacity in the system of capacitance will be
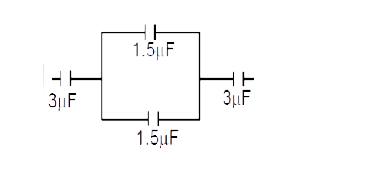 A1μFB2μFC1.5μFD3μF
A1μFB2μFC1.5μFD3μF - Question 2 - Select One
When two capacitors are connected in series, the equivalent capacitance is 154μF. When they are connected in parallel, the equivalent capacitance is 16μF. The individual capacitance are
A5μF,11μFB6μF,10μFC4μF,12μFD8μF,8μF - Question 3 - Select One
The equivalent capacity of n identical condensers each of capacity C connented in series is given by
An2CBnCCnCDCn
If each capacity has capacitance C , then equivalent capacitance between A and B is
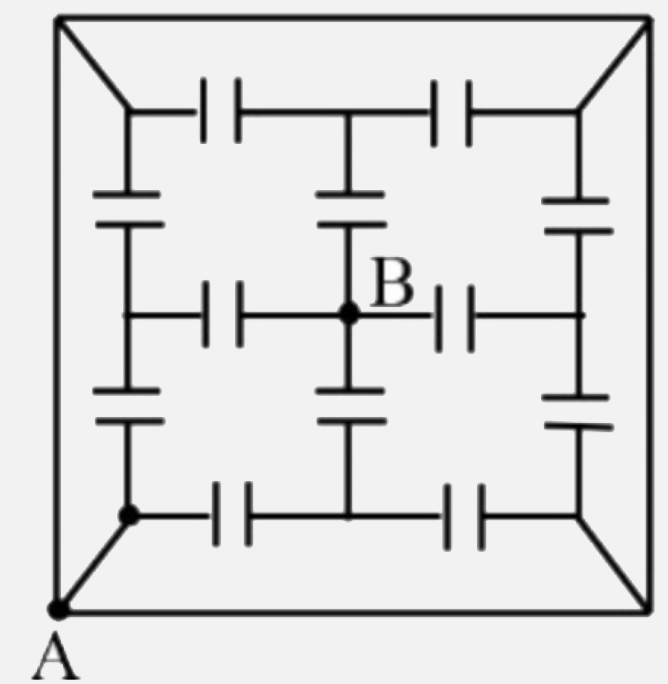 View Solution
View SolutionFind an expression for the equivalent capacitance of a combination of three capacitors in series .
View SolutionThe density of two spheres of equal radius are in the ratio 1:3 and their specific heat capacities in the ratio 2:1 what is the ratio of their heat capacities?
View SolutionThe density of two spheres of equal radius are in the ratio 1:3 and their specific heat capacities in the ratio 2:1 what is the ratio of their heat capacities?
View SolutionTwo equal capacitors are first connected in series and then in parallel. The ratio of the equivalent capacities in the two cases will be:
View Solution

