Four point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
Q = - q
Q=−1q
Q = q
Q=1q
The correct Answer is:A

Let a be the side length of the square ABCD.
∴AC=BD=√a2+a2=a√2
OA=OB=OC=OD=a√22=a√2
Potential is a scalar quantity.
Potential at the centre O due to given charge configuration is
V=14πε0⎡⎢
⎢⎣(−Q)(a√2)+(−q)(a√2)+(2q)(a√2)+(2Q)(a√2)⎤⎥
⎥⎦=0
⇒−Q−q+2q+2Q=0 or Q = -q
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET VITALS18videos
ELECTROSTATICS
- BOOK - MTG GUIDECHAPTER - ELECTRONIC DEVICESEXERCISE - AIPMT/NEET (MCQs)42videos
ELECTRONIC DEVICES
- BOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)48videos
MAGNETIC EFFECTS OF CURRENT AND MAGNETISM
Similar Questions
Four point charges q1,q2,q3 and q4 are placed at the corners of the squares of side a,as shown in figure.Calculate the potential at the centre of the square.
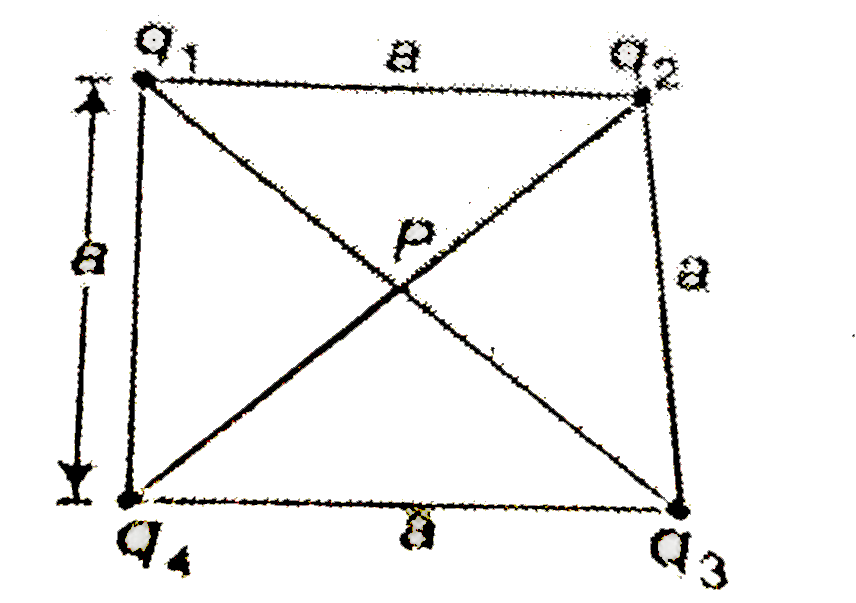
(Given, q1=1×10−8C,q2=−2×10−8C,q3=3×10−8C,q4=2×10−8C and a=1m)View SolutionTwo point charges +Q each are placed at adjacent corners of a square. Other two point charges -Q each are placed at the remaining two corners of the same square . The side of the square is l. Find electric field intensity at the centre of the square.
View Solution
Knowledge Check
- Question 1 - Select One
Four point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
AQ=−qBQ=1qCQ=qDQ=1q - Question 2 - Select One
Four charges Q-Q, Q-Q are placed at the corners of a square as shown . The potential is zero at points
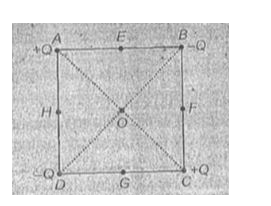 AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO only
AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO only - Question 3 - Select One
Charges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
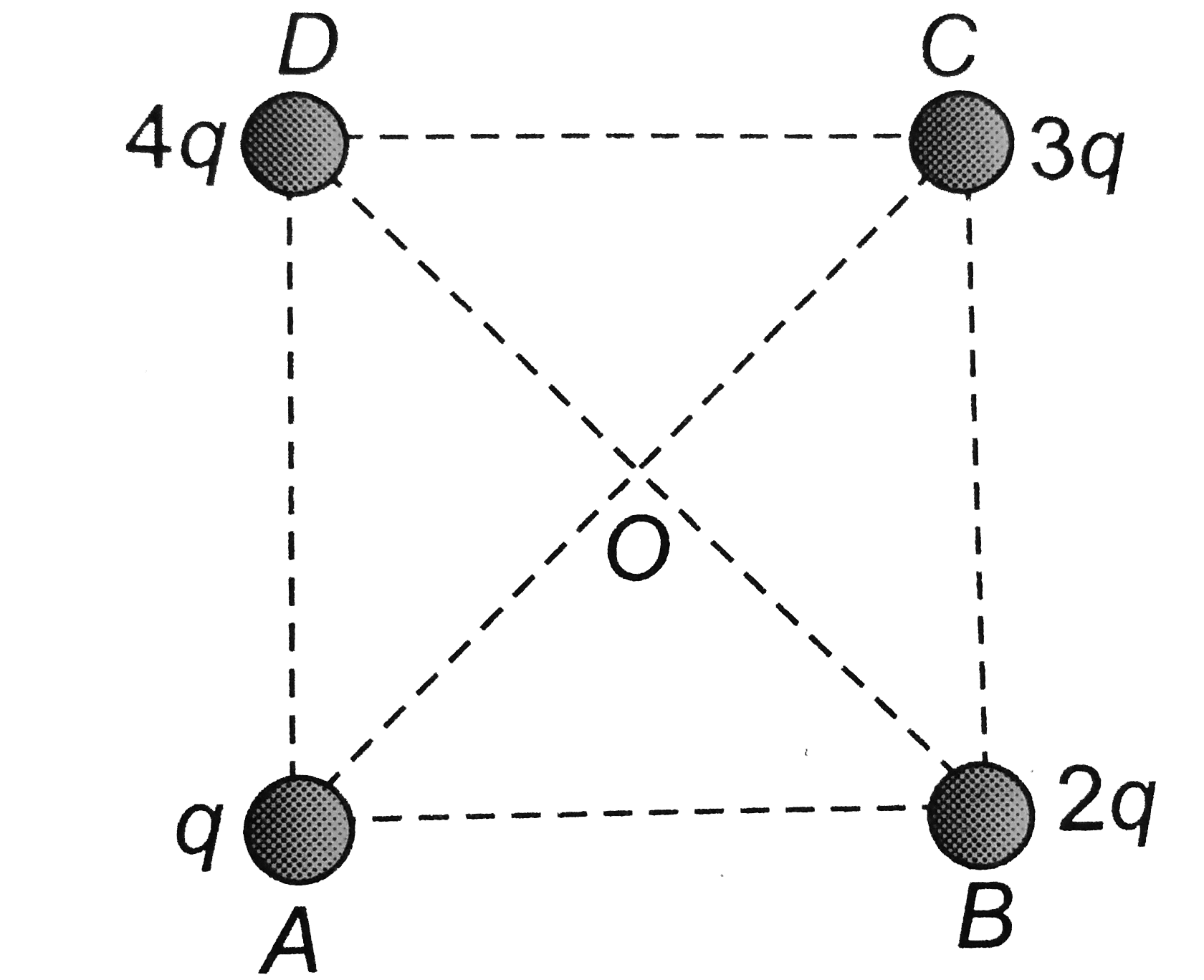 AABBCBCBDDAC
AABBCBCBDDAC
Four charges +q,+2q,+3q and +4q are placed at the four corners ABCD of a square of side a. Calculate the field and potential at the centre of the square.
View SolutionFour charge Q,q,Q and q are kept at the four corners of a square as shown below. What is the relation between Q and q, so that the net force on a charge q is zero ?
 View Solution
View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
potential energy of this system .View SolutionFour point charges Q.q Q and q are placed at the corners of a square side 'a' as shown in the figures.

Find the Potential energy of this system.View SolutionFour point charges Q , q Q and q are placed at the corners of a square of side 'a' as shown in the Fig. Find the
resultant electric force on a charge QView Solution

