A metallic wire of resistance 12Ω is bent of form a square. The resistance between two diagonal points would be
12Ω
24Ω
6Ω
3Ω
The correct Answer is:D
To find the resistance between two diagonal points of a square formed by bending a metallic wire of resistance 12Ω, we can follow these steps:
Step 1: Understand the Length of the Wire
The total resistance of the wire is given as 12Ω. When the wire is bent into a square shape, the length of each side of the square can be determined.
Let the total length of the wire be L. Since the wire is bent into a square, the length of each side of the square will be:
Length of one side=L4
Step 2: Calculate the Resistance of Each Side
The resistance of a segment of wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
Since the total resistance of the wire is 12Ω, and the wire is now divided into four equal segments (one for each side of the square), the resistance of each side of the square will be:
Rside=Rtotal4=12Ω4=3Ω
Step 3: Analyze the Configuration of the Square
When we look at the square, we need to find the equivalent resistance between two opposite corners (diagonal points).
Step 4: Identify the Series and Parallel Connections
From one corner to the opposite corner, the current can travel through two paths:
1. From the first corner to the second corner (through two sides in series).
2. From the first corner to the third corner (through the other two sides in series).
Each path consists of two resistors in series:
Rpath=Rside+Rside=3Ω+3Ω=6Ω
Step 5: Calculate the Equivalent Resistance
Now, we have two paths, each with a resistance of 6Ω, connected in parallel. The equivalent resistance Req for two resistors in parallel is given by:
1Req=1R1+1R2
Substituting the values:
1Req=16+16=26=13
Thus,
Req=3Ω
Conclusion
The equivalent resistance between the two diagonal points of the square formed by the wire is:
3Ω
The total resistance of the wire is given as 12Ω. When the wire is bent into a square shape, the length of each side of the square can be determined.
Length of one side=L4
The resistance of a segment of wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
Rside=Rtotal4=12Ω4=3Ω
When we look at the square, we need to find the equivalent resistance between two opposite corners (diagonal points).
From one corner to the opposite corner, the current can travel through two paths:
1. From the first corner to the second corner (through two sides in series).
2. From the first corner to the third corner (through the other two sides in series).
Rpath=Rside+Rside=3Ω+3Ω=6Ω
Now, we have two paths, each with a resistance of 6Ω, connected in parallel. The equivalent resistance Req for two resistors in parallel is given by:
1Req=1R1+1R2
Substituting the values:
1Req=16+16=26=13
Thus,
Req=3Ω
The equivalent resistance between the two diagonal points of the square formed by the wire is:
3Ω
Topper's Solved these Questions
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - CHECK YOUR NEET VITALS
16 Videos
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - MCQs AIPMT / NEET
32 Videos
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - MCQs AIPMT / NEET
32 Videos
- ATOMS AND NUCLEIBOOK - MTG GUIDECHAPTER - ATOMS AND NUCLEIEXERCISE - AIPMT/NEET(MCQs)
40 Videos
- DUAL NATURE OF MATTER AND RADIATION BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs
30 Videos
Similar Questions
A uniform wire of resistance 36Ω is bent in the form of a circle. The Effective resistance between A and B is (O is the centre of circle):

View Solution(a) Justify the following statements
(i) Tungsten is used exclusively for filament by electric lamps
(ii) We do not use series arrangement for domestic circuits.
(b) A wire of resistance 8Ω is bent in the form of a closed circle. What is the effective resistance between two points A and B at the ends of any diameter of the circle ?
View Solution
Knowledge Check
A metallic wire of resistance 12Ω is bent to form a square. The resistance between two diagonal points would be
A12ΩB24ΩC6ΩD3ΩTwelve wires, each of resistance 6Ω are connected to form a cube. The effective resistance between two diagonally opposite corners of the cube is
A6ΩB12ΩC5ΩD10ΩA wire of resistance 10(Ω)is bent to form a complete circle.Find its resistance between two diametrically opposite points.
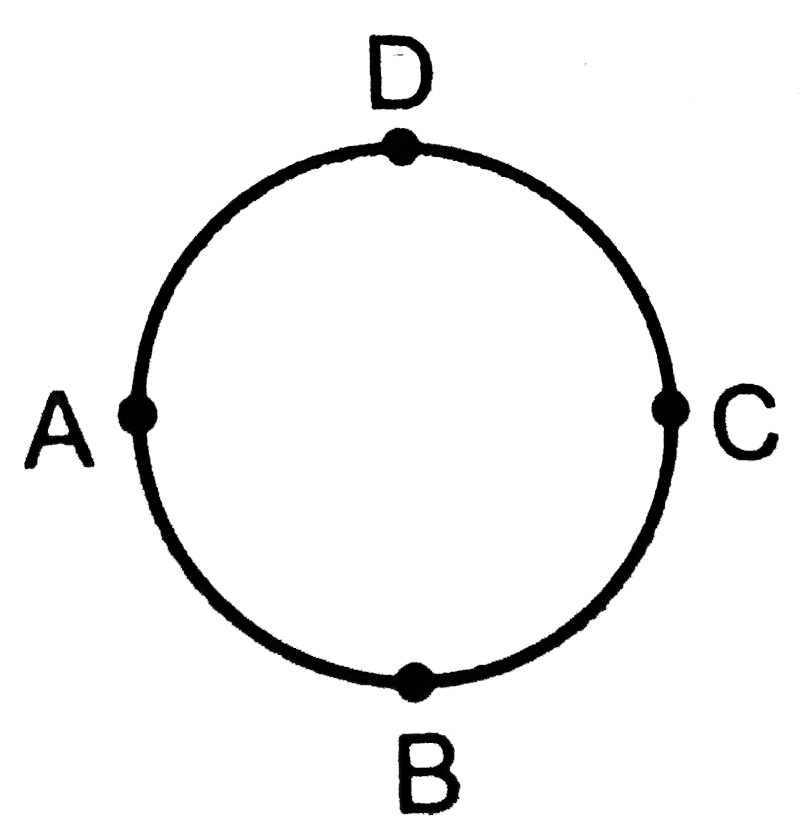 A1.5B2.5C3.5D4.5
A1.5B2.5C3.5D4.5
A wire has resistance 12Ω. It is bent in the form of a circle. The effective resistance between two points across a diameter is.
View SolutionA uniform wire os resistance 12Ω is bent to form a circle. Effective resistance across two diametrically opposite points is
View SolutionA Wire of resistance 12 ohm is bent in the form of a circular ring. The effective resistance between the two points on any diameter of the circle is :
View SolutionA wire has resistance 12Ω. It is bent in the form of a circle. The effective resistance between two points across a diameter is.
View SolutionA wire has resistance of 24Ω is bent in the following shape. The effective resistance between A and B is
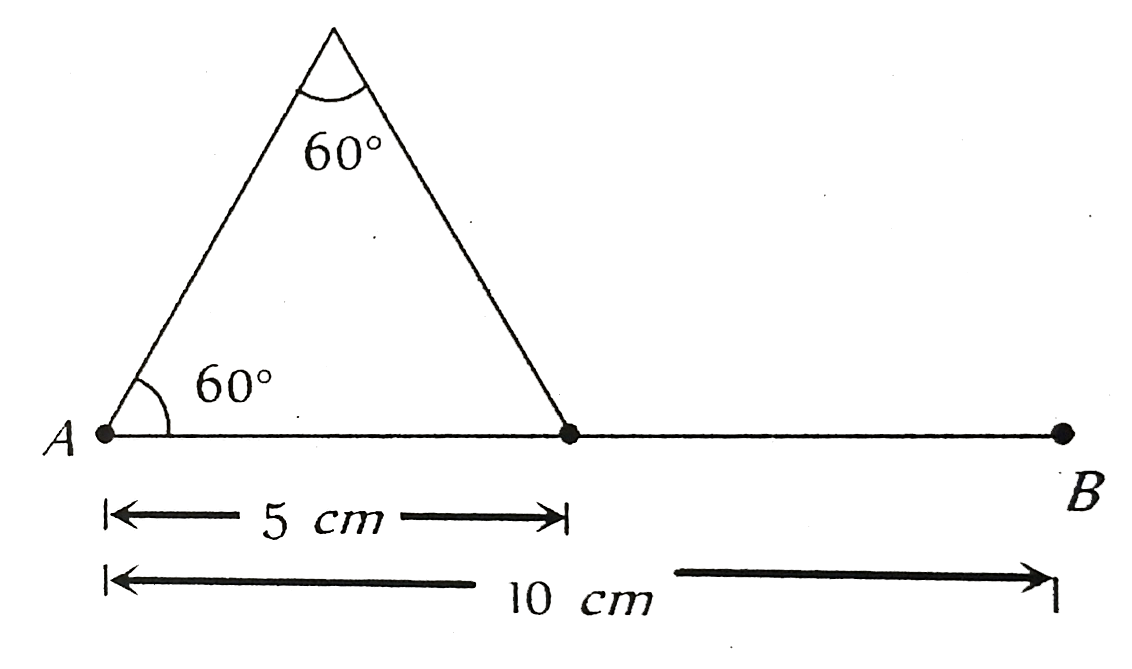
View Solution
