Four indentical mirrors are made to stand vertically to form a square arrangement as shown in a top view. A ray starts from the midpoint M of mirror AD and after two reflections reaches corner D. Then, angle must be

The correct Answer is:B
The ray starting from point M at an angle reaches the corner D at the right along a parallel path. Let a be the length of the side.
From figure,
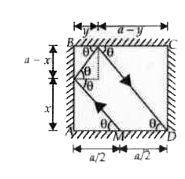
...(i)
...(ii)
...(iii)
From (i) and (ii), we get
...(iv)
From (ii) and (iii), we get
(Using(iv))
Substituting this value of x in equation (i), we get
or
Topper's Solved these Questions
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - Check your NEET vitals
25 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
- OPTICSBOOK - MTG GUIDECHAPTER - OPTICSEXERCISE - AIPMT/NEET
55 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
Two plane mirrors M1 and M2 are inclined at angle as shown in Figure . A ray of light1, which is parallel to M1 , strike M2 and after two reflections, ray 2 becomes parallel to M2. Find the angle θ .
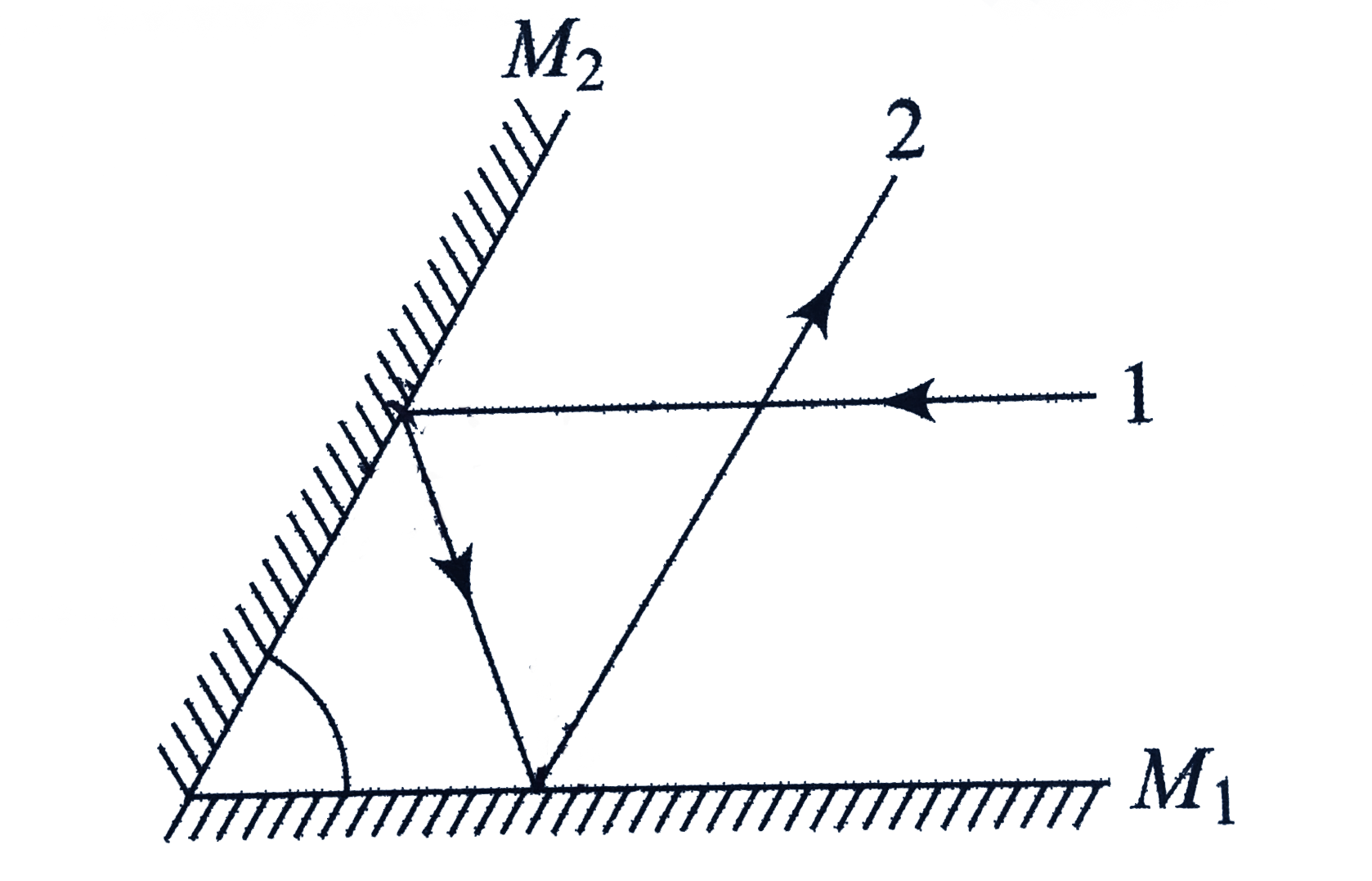
View SolutionTwo mirrors are inclined at angle θ as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if

View Solution
Knowledge Check
Four identical mirror are made to stand vertically to form a square arrangement as shown in a top view. A ray starts from the midpoint M of mirror AD and after two reflections reaches corner D. Then, angle θ must be
 Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)
Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)Four identical mirror are made to stand vertically to form a square arrangement as shown in a top view. A ray starts from the midpoint M of mirror AD and after two reflections reaches corner D. Then, angle θ must be
 Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)
Atan−1(0.75)Bcot−1(0.75)Csin−1(0.75)Dcos−1(0.75)Two plane mirrors M1 and M2 are inclined at angle as shown in Figure . A ray of light1, which is parallel to M1 , strike M2 and after two reflections, ray 2 becomes parallel to M2. Find the angle θ .
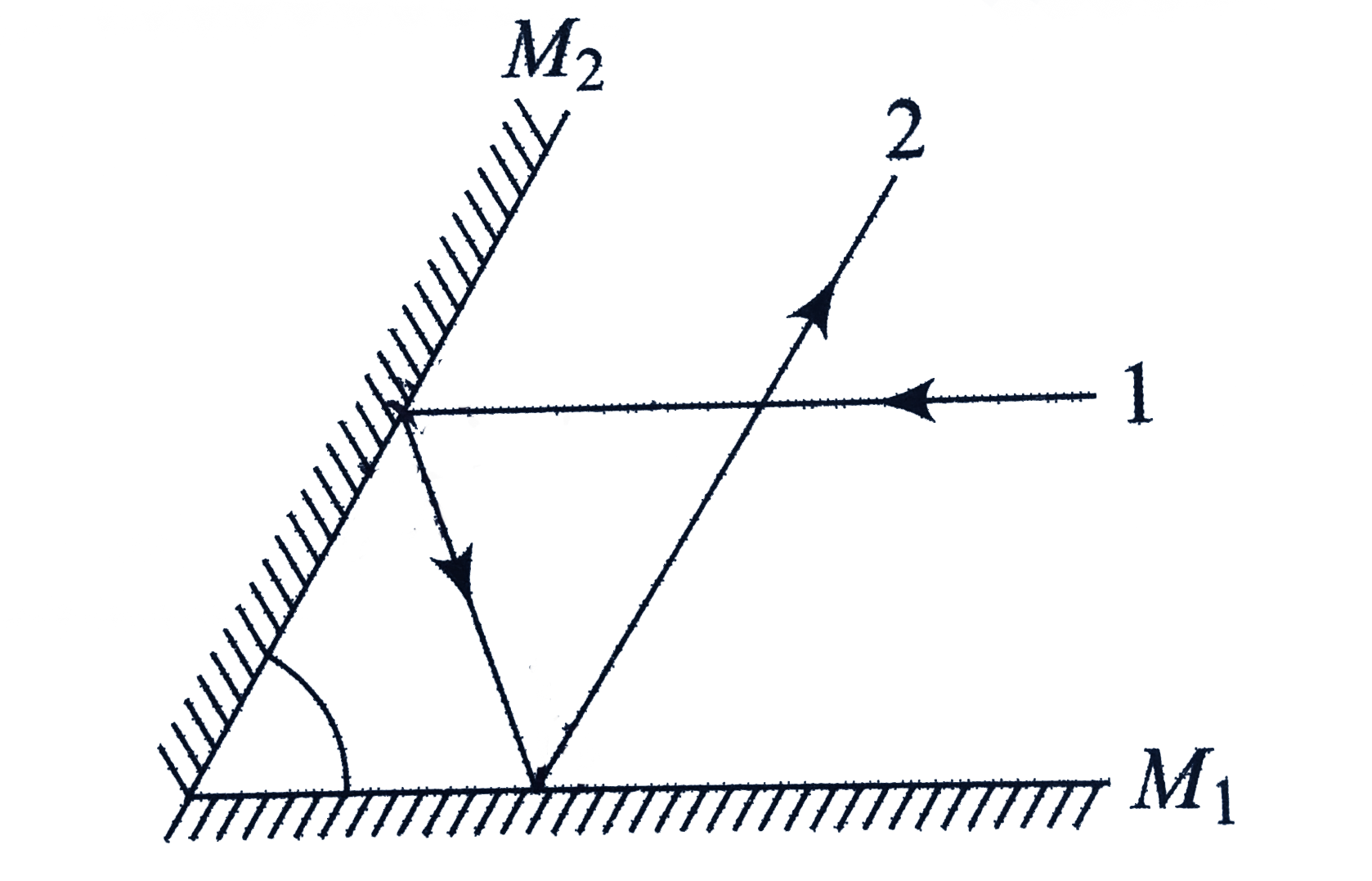 A0∘B30∘C45∘D60∘
A0∘B30∘C45∘D60∘
Two plane mirrors are inclined at angle θ as shown in figure. If a ray parallel to OB strikes the other mirror at P and finally emerges parallel to OA after two reflections then θ is equal to
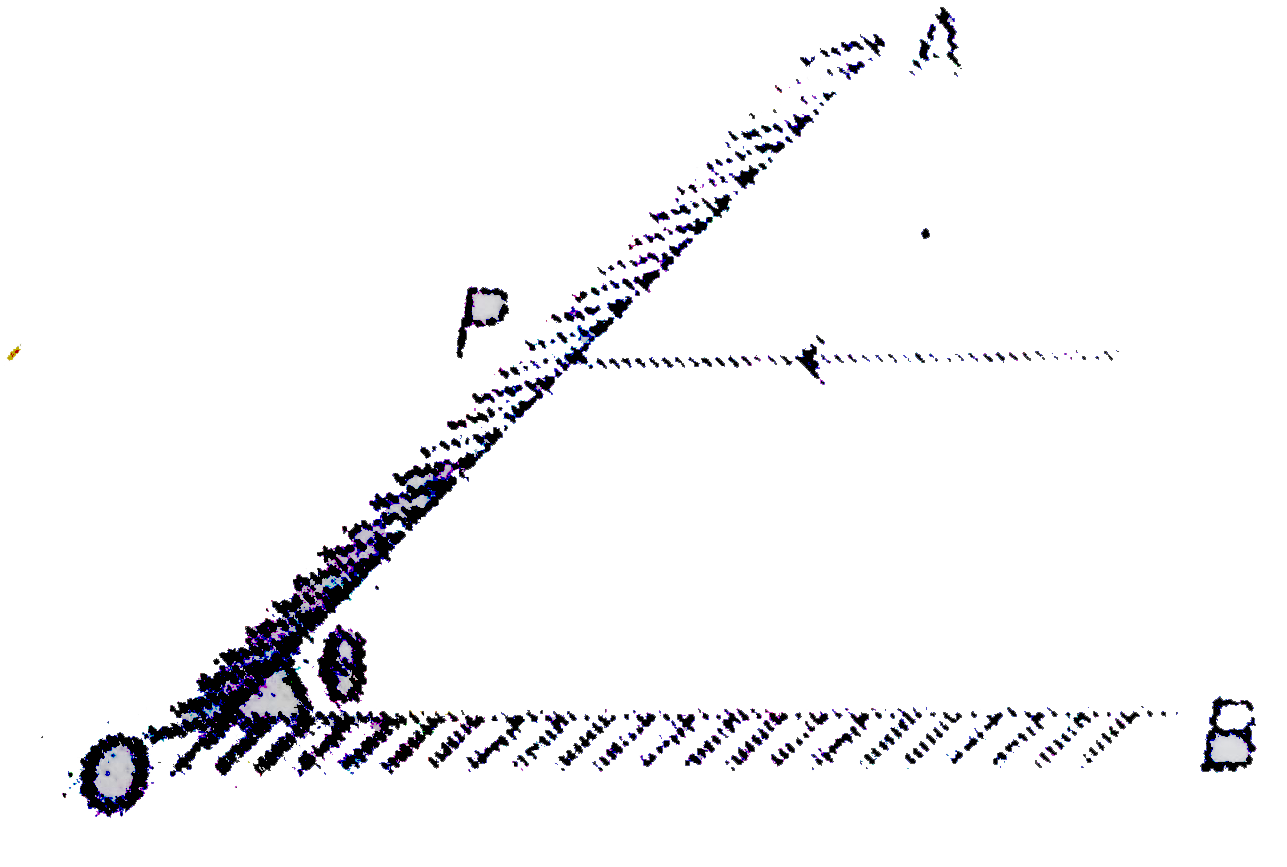
View SolutionTwo plane mirrors are placed at an angle θso that a ray parallel to one mirror gets reflected parallel to second mirror after two consecutive reflections .The value of θwill be-
View SolutionTwo mirrors are inclined at angle θ as shown in figure. Light rays are incident parallel to one of mirrors. Light will start retracing its path after the reflection if

View SolutionTwo plane mirrors subtend an angle θ. Light incident on one mirror after reflection from the other mirror returns parallel to the original direction. The angle θ must be
View SolutionTwo plane mirrors are inclined at angle θ as shown in figure. If a ray parallel to OB strikes the other mirror at P and finally emerges parallel to OA after two reflections then θ is equal to

View Solution
