दिया गया है। cos2mθcos2m+1θ...cos2nθ=sin2n+1θ2n−m+1sin2mθ जहाँ 2mθ≠kπ,n,m,kεI निम्न को हल करें।
sin9π/14sin11π/14sin13π/14 बराबर है
1/64
−1/64
1/8
−1/8
The correct Answer is:C
Topper's Solved these Questions
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Integer type questions)
2 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Reasoning type questions)
1 Videos
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - JEE Advanced
47 Videos
- त्रिविमीय निर्देशांक ज्यामिति BOOK - ERRORLESS HINDICHAPTER - त्रिविमीय निर्देशांक ज्यामिति EXERCISE - JEE ADVANCED (Matrix Match type questions)
4 Videos
Similar Questions
व्यंजक 1sin2θ+3sinθcosθ+5cos2θ का अधिकतम मान ज्ञात कीजिए |
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
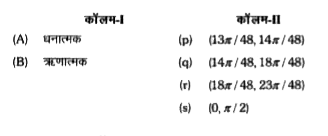
View Solutionमाना कि α,β,γ>0 तथा α+β+γ=π2 है।
कथन-1 : ∣∣∣tanαtanβ−a!6∣∣∣+∣∣∣tanβtanγ−b!2∣∣∣+∣∣∣tanγtanα−c!3∣∣∣≤0 जहाँ n≠1.2….n, तब, tanαtanβ,tanβtanγ,tanγtanα स.श्रे. में है।
कथन-2 : tanαtanβ+tanβtanγ+tanγtanα=1
View Solution0<θ<π2 के लिए 6Σm=1cosec(θ+(m−1)π4)cosec(θ+mπ4)=4√2 का के हल निम्न है।
View Solutionमाना निम्न रैखिक समीकरण है ax+by+cz=0,bx+cy+oz=0,cx+ay+bz=0 कॉलम । में दी गयी स्थितियों/व्यंजकों का कॉलम ॥ में दिए गए वक्तव्यों से सुमेल करें

View SolutionIf(cos theta+i sin theta)(cos2 theta+i sin2 theta).....(cos n theta+i sin n theta)=1 then the value of theta is:
View SolutionIf θ=π2n+1 , prove that: 2ncosθcos2θcos22cos2n−1θ=1.
View Solutionif m*tan(theta-30)=n*tan(theta+120), show that cos2 theta=(m+n)/(2(m-n))
View Solutionm tan(theta-30^(@))=n tan(theta+120^(@)) show that cos2 theta=(m+n)/(2(m-n))
View SolutionIf m and n are positive integers satisfying 1+cos2 theta+cos4 theta+cos6 theta+cos8 theta+cos10 theta=(cos m theta*sin n theta)/(sin theta) then (m+n) is equal to
View Solution(1+sin2 theta-cos2 theta)/(1+sin2 theta+cos2 theta)=tan theta
View SolutionUsing induction,prove that cos theta cos2 theta cos2^(2)theta...cos2^(n-1)theta=(sin2^(n)theta)/(2^(n)sin theta)
View SolutionIf (2^(n)+1)theta=pi then 2^(n)cos theta cos2 theta cos2^(2)theta......cos2^(n-1)theta=
View SolutionIf A=[cos2θsin2θ−sin2θcos2θ] , find A2 .
View SolutionIf cosθ>sinθ>0 then I=∫ [ln[1+sin2θ1−sin2θ]cos2θ+ln[cos2θ1+sin2θ]]=Ksin2θ ln[cosθ+sinθcosθ−sinθ]+mln|cos2θ|+c , then k+m=
View Solution
