If the symbols have usual meanings then gR2M represents
G
G2
1G
1G2
The correct Answer is:A
To solve the problem, we need to analyze the expression (gR2)/M and determine what it represents, given that the symbols have their usual meanings in physics.
1. Understand the Symbols:
- g = acceleration due to gravity at the surface of the Earth (approximately 9.81m/s2).
- R = radius of the Earth (approximately 6.371×106m).
- M = mass of the Earth (approximately 5.972×1024kg).
- G = universal gravitational constant (6.674×10−11N m2/kg2).
2. Recall the Formula for g:
The acceleration due to gravity g at the surface of a planet can be expressed using the formula:
g=GMR2
where G is the universal gravitational constant, M is the mass of the planet, and R is the radius of the planet.
3. Rearranging the Formula:
We can rearrange this formula to express G:
G=gR2M
This shows that G can be calculated if we know g, R, and M.
4. Substituting into the Expression:
The expression given in the question is gR2M. From our rearrangement, we see that:
gR2M=G
Thus, the expression gR2M represents the universal gravitational constant G.
5. Conclusion:
Therefore, the expression gR2M represents the universal gravitational constant G.
Final Answer:
gR2M represents the universal gravitational constant G.
- g = acceleration due to gravity at the surface of the Earth (approximately 9.81m/s2).
- R = radius of the Earth (approximately 6.371×106m).
- M = mass of the Earth (approximately 5.972×1024kg).
- G = universal gravitational constant (6.674×10−11N m2/kg2).
The acceleration due to gravity g at the surface of a planet can be expressed using the formula:
g=GMR2
where G is the universal gravitational constant, M is the mass of the planet, and R is the radius of the planet.
We can rearrange this formula to express G:
G=gR2M
This shows that G can be calculated if we know g, R, and M.
The expression given in the question is gR2M. From our rearrangement, we see that:
gR2M=G
Thus, the expression gR2M represents the universal gravitational constant G.
Therefore, the expression gR2M represents the universal gravitational constant G.
gR2M represents the universal gravitational constant G.
Topper's Solved these Questions
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - HIGHER ORDER THINKING QUESTIONS25videos
GRAVITATION
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - ELECTRIC CURRENT EXERCISE - HIGHER ORDER THINKING QUESTIONS29videos
ELECTRIC CURRENT
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - HEATEXERCISE - HIGHER ORDER THINKING QUESTIONS15videos
HEAT
Similar Questions
Knowledge Check
- Question 1 - Select One
If the symbols have their usual meanings ,GMR2 is equal to
Ag2B1g2CgD1g - Question 2 - Select One
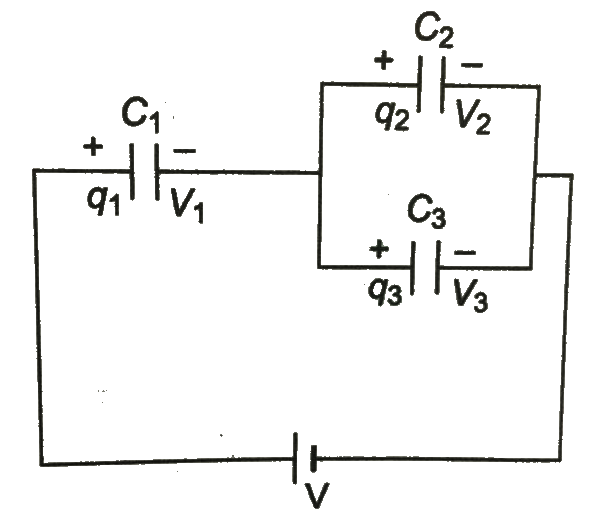
In three capacitors C1,C2, and C3, are joined to a battery, With symbols having their usual meaning, the correct conditions will be
 .AQ1=Q2=Q3 and
.AQ1=Q2=Q3 and
V1=V2=V3=VBQ1=Q2+Q3 and
V=V1+V2+V3CQ1=Q2+Q3 and V=V1+V2DQ2=Q3 and V2=V3 - Question 3 - Select One
What is the height of a geostationary satellite in terms of M, R, G and T? (T=Length of the day and the other symbols have their usual meanings in the following options.)
A(GMT24π2)1/3+RB(GMT24π2)1/3−RC(4π2GMT2)1/3D(4πGMR2)1/3−R
In the circuit as shown in figure if all the symbols have their usual meanings, then identify the correct statements,
 View Solution
View SolutionThe Kirchhoff's first law (Σi=0) and second law (ΣiR=ΣE), where the symbols have their usual meanings, are respectively based on
View SolutionIn the following 'I' refers to current and other symbols have their usual meaning. Chosse the option that corresponds to the dimensions of electrical conductivity:
View SolutionIn YDSE, find the missing wavelength at y=d, where symbols have their usual meaning (takeD>>d).
View SolutionIf all symbols have their usual meaning, then for a non-volatile non-electrolyte solute Ltm→0(ΔTfm) is equal to
View Solution

