If the frequency of a wave is doubled, its wavelength
becomes doubled
remains same
becomes half of the original
none of these
The correct Answer is:C
To solve the problem of how the wavelength of a wave changes when its frequency is doubled, we can follow these steps:
1. Understand the Relationship Between Speed, Frequency, and Wavelength:
The speed of a wave (v) is given by the equation:
v=f⋅λ
where f is the frequency and λ is the wavelength.
2. Assume Constant Speed:
For this problem, we will assume that the speed of the wave remains constant. This means that if we change the frequency, the wavelength must change accordingly to maintain the equation.
3. Initial Conditions:
Let the initial frequency be f and the initial wavelength be λ. Therefore, we can express the speed of the wave as:
v=f⋅λ
4. Doubling the Frequency:
If the frequency is doubled, the new frequency becomes:
f′=2f
We need to find the new wavelength λ′ when the frequency is doubled.
5. Using the Wave Speed Equation:
Since the speed of the wave remains constant, we can write:
v=f′⋅λ′
Substituting f′=2f into the equation gives:
v=2f⋅λ′
6. Setting the Two Speed Equations Equal:
Since both expressions equal the wave speed v, we can set them equal to each other:
f⋅λ=2f⋅λ′
7. Canceling f:
Assuming f is not zero, we can divide both sides by f:
λ=2⋅λ′
8. Solving for the New Wavelength:
Rearranging the equation gives:
λ′=λ2
This means that the new wavelength λ′ is half of the original wavelength λ.
Conclusion:
If the frequency of a wave is doubled, its wavelength is halved. Thus, the answer is:
λ′=λ2
The speed of a wave (v) is given by the equation:
v=f⋅λ
where f is the frequency and λ is the wavelength.
For this problem, we will assume that the speed of the wave remains constant. This means that if we change the frequency, the wavelength must change accordingly to maintain the equation.
Let the initial frequency be f and the initial wavelength be λ. Therefore, we can express the speed of the wave as:
v=f⋅λ
If the frequency is doubled, the new frequency becomes:
f′=2f
We need to find the new wavelength λ′ when the frequency is doubled.
Since the speed of the wave remains constant, we can write:
v=f′⋅λ′
Substituting f′=2f into the equation gives:
v=2f⋅λ′
Since both expressions equal the wave speed v, we can set them equal to each other:
f⋅λ=2f⋅λ′
Assuming f is not zero, we can divide both sides by f:
λ=2⋅λ′
Rearranging the equation gives:
λ′=λ2
This means that the new wavelength λ′ is half of the original wavelength λ.
If the frequency of a wave is doubled, its wavelength is halved. Thus, the answer is:
λ′=λ2
Topper's Solved these Questions
- WAVE MOTION AND SOUND BOOK - MCGROW HILL PUBLICATIONCHAPTER - WAVE MOTION AND SOUND EXERCISE - HIGH ORDER THINKING QUESTIONS
22 Videos
- SOURCES OF ENERGY BOOK - MCGROW HILL PUBLICATIONCHAPTER - SOURCES OF ENERGY EXERCISE - ELEMENTARY QUESTIONS
82 Videos
- WORK AND ENERGYBOOK - MCGROW HILL PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING QUESTIONS
29 Videos
Similar Questions
The picture shows a wave generated in a laboratory
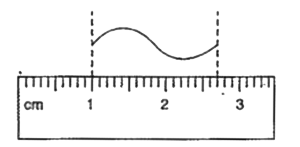
If the frequency of the wave shown were doubled, what would be the wavelength of the wave ?
View SolutionThe frequency of a sound wave is 200 Hz and its wavelength is 150 cm. What is the distance travelled by a sound wave in the time taken to produce 150 waves ?
View Solution
Knowledge Check
A plane electromagnetic wave travels in vacuum along z-direction. If the frequency of the wave is 40 MHz then its wavelength is
A5 mB7.5 mC8.5 mD10 mThe frequency of radio waves corresponding to wavelength of 20 m is
A3×107HzB1.5×107 HzC5×10−7HzD3×106HzThe frequency of a sound wave is related to its
AAmplitudeBLoudnessCPitchDQuality
The frequency of a sound wave is 200 Hz and its wavelength is 150 cm. What is the distance travelled by a sound wave in the time taken to produce 150 waves ?
View SolutionFrequency of an E.M. waves is 10 MHz then its wavelength is :
View SolutionIf the frequency of a wave is increased by 25%, then the change in its wavelength will be: (medium not changed)
View SolutionThe frequency of radio waves corresponding to a wavelength of 10 m is
View SolutionIf the frequency of a wave is 330 Hz, and velocity of wave in air is 330 m s−1, then, the wavelength of the wave is
View Solution
