During the fission of 235U , energy of the order of 180 MeV is generated per nucleus fissioned . The amount of energy released by the fission of 0.235 g of 235U is : Solution in Telugu
1.73×107kJ
1.08×1025 kJ
1.73×1010J
1.08×107kJ
The correct Answer is:A, C
1 nuclide → 180 Me V , (0.235235×N0)→Q=?
Q=0.235×6×1023×180235×1=1080×1020MeV
Q=1.080×1023MeV=1.080×1023×106×1.602×10−191000KJ
= (1.73×1023+6−19−3)=1.73×107KJ
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR CHEMISTRY EXERCISE - LECTURE SHEET (LEVEL- II) (EXERCISE - II) (Linked Comprehension type questions)9videos
NUCLEAR CHEMISTRY
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR CHEMISTRY EXERCISE - LECTURE SHEET (LEVEL- II) (EXERCISE - III) (Match the following questions )3videos
NUCLEAR CHEMISTRY
- BOOK - AAKASH SERIESCHAPTER - NOBLE GASESEXERCISE - PRACTICE SHEET - 2 (Single more than one option questions)5videos
NOBLE GASES
- BOOK - AAKASH SERIESCHAPTER - PERIODIC TABLEEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS37videos
PERIODIC TABLE
Similar Questions
Radioactive decay is a statisticle process i.e., we cannot precisely predict the timing of a particular radioactivity of a particular nucleus . The nucleus can disintegrate immediately or it may take infinite time . Simply the probability of the number of nuclei being disintegrated at any instant can be predicted . the rate at which a particular decay process in a radioactive sample is directly proportional to the number of radioactive nuclei present and thus obeys first order kinetics . the factor dN/N expresses the fraction of nuclei decayed in time dt.t1/2 is the time in which half of the atoms are decayed and average life is the time for the nucleus to survive before decay .
Which of the following relation is correct ? (t1/2 and t3/4 are time required to complete half and 3/4 decay respectively )02:40View SolutionMatch the Column - I Radio-isotope with Column - II medicinal use and select correct matching :
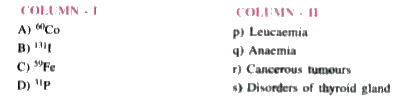 01:59View Solution
01:59View SolutionWhich compound is prepared by the following reaction :Xe+2F2Ni vessel−−−−−−−−→673K,5−6atm1:5volume ratio
01:49View SolutionWrite on the IUPAC nomenclature of the elements with atomic number greater than 103.
01:57View SolutionCalculate the energy released by fission from 2g of .235.92U in kWh. Given that the energy released per fission is 200MeV.
02:50View SolutionCalculate the energy released by the fission 1g of .235U in joule, given that the energy released per fission is 200MeV.
(Avogadro's number =6.023×1023)04:15View SolutionThe energy released per fission of uranium 235 is about 200 MeV. A reactor using U-235 as fuel is producing 1000 kilowatt power. The number of U-235 nuclei undergoing fission per sec is, approximately-
04:41View SolutionDuring the fission of U-235, energy of the order of 180 MeV is generated per nucleus fissioned . The amount of energy released by the fission of 0.235 g of U-235 is
View SolutionThe energy released when one nucleus of .92u235 undergoes fission is 188 MeV. The energy released when 100g of undergoes fission is .92u235
View SolutionDuring the fission of U-235, a large amount of energy of the order of 180 MeV is generated per nucleus fissioned. The amount of energy released by the fission of 0.235 g of U-235 is :
View SolutionOne kilogram U^(235) Is free energy at total fission (if 200 MeV energy is released at fission of 1 nucleus).
View SolutionWhen U-235 undergoes fission, 0.1% of its mass is converted into energy. Then amount of energy released during the fission of 1kg of uranium-235 will be
02:29View SolutionEnergy released during the fission of one Uranium-235 nucleus is 200MeV. Energy released by the fission of 500gm of U-235 nuclei will be about
01:57View SolutionCalculate the energy released by fission from 2 g of 23592U in k Wh. Given that the energy released per fission is 200 Mev.
02:59View SolutionThe average energy released in the fission of is U235 is
03:09View Solution

