A radioactive sample had an initial activity of 56 dpm . After 69.3 minutes , it was found to have an activity of 28 dpm , the number of atoms in a sample having an activity of 100 dpm is 10x . The value of x is ……. Solution in Telugu
The correct Answer is:4
56 dpm t1/2=69.3min−−−−−−−−→28d±A=λN,100=(0.69369.3),Nt,Nt=104
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR CHEMISTRY EXERCISE - PRACTICE SHEET - 1 (Single or more than one option questions)15videos
NUCLEAR CHEMISTRY
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR CHEMISTRY EXERCISE - PRACTICE SHEET - 1 (Linked Comprehension type questions )6videos
NUCLEAR CHEMISTRY
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR CHEMISTRY EXERCISE - LECTURE SHEET (LEVEL- II) (EXERCISE - III) (Match the following questions )3videos
NUCLEAR CHEMISTRY
- BOOK - AAKASH SERIESCHAPTER - NOBLE GASESEXERCISE - PRACTICE SHEET - 2 (Single more than one option questions)5videos
NOBLE GASES
- BOOK - AAKASH SERIESCHAPTER - PERIODIC TABLEEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS37videos
PERIODIC TABLE
Similar Questions
The triad of nuclei that represents isotopes is :
01:53View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure . The rate of radioactive disintegration (Activity) is represented as −dNdt=λN , Where λ = decay constant , N number of nuclei at time t , N0 = initial no. of nuclei.
The above equation after integration can be represented as λ=2.303tlog(N0N)
Half-life period of U232 is 2.5×105 years . In how much time will the amount of U237 remaining be only 25% of the original amount ?01:30View SolutionMatch the Column - I Radio-isotope with Column - II medicinal use and select correct matching :
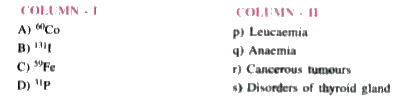 05:23View Solution
05:23View SolutionWhich compound is prepared by the following reaction :Xe+2F2Ni vessel−−−−−−−−→673K,5−6atm1:5volume ratio
00:49View SolutionWrite on the IUPAC nomenclature of the elements with atomic number greater than 103.
00:37View SolutionThe disintegrationn rate of a certain radioactive sample at any instant is 4750 dpm which becomes 2700 dpm 5 min later. Calculate the half life to sample?
View SolutionA radioactive isotope has initial activity of 28 dpm Its activity is reduced to 14 dpm after half an hour. The initial number of nuclide in sample was:
03:41View SolutionThe rate of disintegration of a certain radioactive sample at any instant is 8100 dpm. Fifty minutes later the rate becomes 2700 dpm. The half of the radioactive sample will be (Take log2=0.3, log3=0.5, log5=0.7 )
02:43View SolutionA radioactive sample had an initial activity of 56 dpm . After 69.3 minutes, it was found to have an activity of 28 dpm . Find the number of atoms in a sample having an activity of 100 dpm.
02:31View SolutionA radioactive sample has initial activity of 28 dpm 30 minutes later its activity 14 dpm . How many atoms of nuclide were present initially?
02:23View SolutionIn order to determine the volume of blood in an animal, a 1.0 mL sample of solution of 10^(3) dpm of ._(1)^(3)H is injected into the animal blood stream. After sufficient time for circulatory equilibrium to be established, 2mL of blood is found to have activity to 10 dpm. The volume of blood in animal is :
02:00View SolutionA radioactive sample has an initial activity of 50 dpm, 20 minute later, the activity is 25 dpm . How many atoms of the radioactivity nuclide were there originally?
03:17View SolutionA radioactivity sample had an initial activity of 56dpm. After 69.3 minutes, it was found to have an activity of 28dpm, the number of atoms in a sampple having an activity of 10dpm, is 10""^(x) . The value of x is
03:37View SolutionThe rate of disintegration of a radioactivity element changes from initial value of 10,000 dpm to 2,500 dpm in 50 days . The decay constant is
03:52View SolutionA radioactive sample had an initial activily of 56 dpm (disintegration per min). After 69.3min it was found to have an activity of 28 dpm. Find the number of atoms in a sample having an activity of 10 dpm.
03:35View Solution

