Match the term (in Column-I) with its expression (in Column-II) :
Solution in Telugu
The correct Answer is:A-R ; B-P; C-S; D-Q
Fomulae for molecular speeds.
Topper's Solved these Questions
- STATES OF MATTERBOOK - AAKASH SERIESCHAPTER - STATES OF MATTEREXERCISE - PRACTICE SHEET (EXERCISE -III) (LEVEL -II ADVANCED)(INTEGER TYPE QUESTIONS)
3 Videos
- STATES OF MATTERBOOK - AAKASH SERIESCHAPTER - STATES OF MATTEREXERCISE - PRACTICE SHEET (EXERCISE -IV) (LEVEL -I MAINS)(STRAIGTH OBJECTIVE TYPE QUESTIONS)
20 Videos
- STATES OF MATTERBOOK - AAKASH SERIESCHAPTER - STATES OF MATTEREXERCISE - PRACTICE SHEET (EXERCISE -III) (LEVEL -II ADVANCED)(LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- SATURATED HYDROCARBONSBOOK - AAKASH SERIESCHAPTER - SATURATED HYDROCARBONSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- STOICHIOMETRYBOOK - AAKASH SERIESCHAPTER - STOICHIOMETRYEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
59 Videos
Similar Questions
Kinetic energy of 0.30 moles of He gas in a container of maximum capacity of 4 litres at 5 atmosphere, must be (R = 0.0821 atm litre mole−1K−1 )________×101 atm.lit
View SolutionThe compressibility factor of an ideal gas is
View SolutionOn the basis of the postulates of kinetic theory of gases, it is possible to derive the mathematical expression, commonly known as kinetic gas equation. PV=13mnu3?
where, P= Pressure of the gas, V a volume of the gas, m=Mass of a molecule, n = Number of molecules present in the given amount of a gas and u = root mean square speed
For one mole of gas, PV = RT and n=NA
13mNau2=RTor23.12mNAu2=NA
[12mNAu2=KEper mole],23K.E.=RT⇒K.E.32RT
Average kinetic energy per mol does not depend on the nature of the gas but depends only on temperature. This, when two gases are mixed at the same temperature, there will be no rise or decrease in temperature unless both react chemically.
Average kinetic energy per molecule = Average K.E. per moleN=32RTN⇒32kT
where k is the Boltzmann constant
In deriving the kinetic gas equation, the use of the root mean square speed of the molecules is done, hecause it is
View SolutionWhy boiling and melting points of hydrocarbons are low ?
View SolutionDistinguish between element and compound?
View SolutionSound is travelling in a long tube towards right and the graph of excess pressure variation Vs position (at some instant) is given below.
 Match velocities in column-I with column-II P,Q,R,S,T are medium particles inside the tube.
Match velocities in column-I with column-II P,Q,R,S,T are medium particles inside the tube.
Column-IColumn-II(A)velocity is towards right(P)P(B)velocity is towards left(Q)Q(C)velocity is zero(R)R(D)Speed is maximum(S)S(T)T
View SolutionMatch the column : A particle at a distance r from the centre of a uniform spherical planet of mass M radius R(lt r) has a velocity v magnitude of which is given in column I. Match trajectory from column II about possible nature of orbit. {:(,"Column I",,"Column II"),((A),0lt V lt sqrt((GM)/(r )),(P),"Straight line"),((B),sqrt((GM)/(r )),(Q),"Circle"),((C ),sqrt((2GM)/(r )),(R ),"Parabola"),((D),v gt sqrt((2GM)/(r )),(S ),"Ellipse"):}
View SolutionFor a monotomic gas at temperature T, match the following columns. {:(,"ColumnI",, "ColumnII"),((A),"Speed of sound", (p),sqrt(2RT//M)),((B),"RMS speed of gas molecules",(q),sqrt(8RT//piM)),((C),"Average speed of gas molecules",(r),sqrt(3RT//M)),((D),"Most probable speed of gas molecules",(s),sqrt(5RT//3M)):}
View SolutionColumn II gives some equations. In these equations x is distance, t is time , m is mass, v is velocity u is initial velocity and F is force . Match the statements in Column I to the equations in Column II.
View SolutionA ball is projected from the ground with velocity v such that its range is maximum. Match the columns. COLUMN-I (A) Velocity at half of the maximum height (B) Velocity at the maximum height (C) Change in its velocity when it returns to the ground (D) Average velocity when it reaches the maximum height. COLUMN-II (P) (sqrt(3)v)/2 (Q) v/sqrt(2) (R) vsqrt(2) (S) v/2sqrt(5/2)
View SolutionMatch the parameters given in column I with the expressions given in column II.
Column IColumn II1. Pressure of a gas(i)KT√2πd2P2. RMS speed of gas molecules (ii)√2KTm3. Mean free path (iii)KT√3πP24. Most probable speed of gas molecules(iv)√3KTm(v)13mnv2(vi)13KT
View SolutionMatch Column - I with Column - II
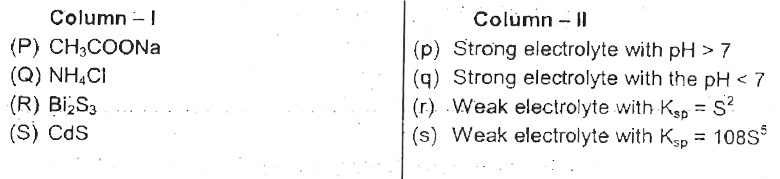
PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionMatch the following: {:("Column-I","Column-II"),((A)" Root mean square velocity",(p) sqrt((3P)/(d))),((B)" Average velocity",(q) sqrt((3RT)/(m))),((C)" Most probable velocity",(r) sqrt((8P)/(pid))),((D)" Velocity possessed by maximum fraction of molecules",(s) sqrt((2RT)/(m))):}
View SolutionMatch the following: {:("Column-I","Column-II"),((P)" R.M.S",(1) (2)/(3)NKT),((Q)" PV",(2) KT ),((R)" Average K.E.",(3) sqrt((3PV)/(M))),((S)" Most probable speed" ,(4) sqrt((2RT)/(M))):}
View SolutionIn Column-I relaion and in Column-II corresponding equation is given. Match them properly : {:("Column-I","Column-II"),((1) Velocity rarr relation,(a)v=v_0+at),((2) Velocity rarr "displacement relation",(b)S=v_0t+1/2at^2),(,(c) v^2=v_(0)^2+2as):}
View Solution
