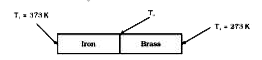
An iron bar (L1=0.1 m,A1=0.02 m2,K1=97 Wm−1K−1) and a brass bar (L2=0.1 m,A2=0.02 m2,K2=109 W m−1K−1) are soldered end to end as shown in figure. The free ends of the iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar, and (iii) the heat current through the compound bar.
 Solution in Gujrati
Solution in Gujrati
Length of iron rod L1=0.1m Area A1=0.02m2
Thermal conductivity K1=79 Wm−1K−1
Heat current =H1
Length of brass rod L2=0.1 m
Area A2=0.02m2
Thermal conductivity K2=109 Wm−1K−1
Temp. of heat and of combined rod T1=373 K
Temp. of cold and of combined rod T2=273K
Temp. of junction T0=?
(i) In thermal steady state H1=H2=H
∴K1A1(T1−T0)L1=K2A2(T0−T2)L2
But A1=A2=A and L1=L2=L
∴K1(T1−T0)=K2(T0−T2)
∴K1T1−K1T0=K2T0−K2T2
∴K1T1+K2T2=T0(K1+K2)
∴T0=K1T1+K2T2K1+K2
=79×373+109×27379+109
=29467+29757188
=59224188
∴T0=315K
(ii) thermal resistance RH=2LKA,RH1=LK1A
and RH2=LK2A
∴ In series connection RH=RH1+RH2
∴2LKA=LK1A+LK2A
∴2K=1K1+1K2
thermal conductivity of combined rod
K=2K1K2K1+K2
=2×79×10979+109
=17222188
∴K=91.6 Wm−1K−1
⇒ (iii) Heat current in combined rod,
H=KA(T1−T2)2L
=91.6×0.02×373−2732×0.1
∴H=916W
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Section - B
10 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Section - B (Numericals) Numerical From Textual Exercise
26 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Information : Higher Order Thinking Skills (HOTS)
8 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-F (SECTION-D) QUESTIONS PAPER
1 Videos
- THERMODYANMICS BOOK - KUMAR PRAKASHANCHAPTER - THERMODYANMICS EXERCISE - Question Paper
11 Videos
Similar Questions
Show that the coefficient of area expansions, (ΔA/A)/ΔT, of a rectangular sheet of the solid is twice its linear expansively, αl.(αl=10−5K−1)
View SolutionThe triple points of neon and carbon dioxide are 24.57 K and 216.55 respectively. Express these temperatures on the Celsius and Fahrenheit scales.
View SolutionWhat is the triple point ?
View SolutionA rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
View SolutionWhy is a steam burn more damaging than a burn with boiling water of the same ?
View SolutionAn iron bar ( L_(1) = 0.1 m, A_(1) = 0.02 m^(2) , K_(1) = 79 Wm^(-1) K^(-1) ) and a brass bar (L_(2)=0.1 m , A_(2) = 0.02 m^(2), K_(2) = 109 Wm^(-1)K^(-1) ) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the juction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar. .
View SolutionA steel bar 10.0 cm long is welded end to end to a copper bae 20.0 cm long. Both bars are insulated perfectly on their sides . Each bar has a separate cross-section, 2.00 cm on a side . The free end of the steel bar is maintained at 100^(@)C by placing it in contact with ice . find the temperature at the junction of the two bars and the total rate of heat flow . thermal conductivity of steel = 50.2 Wm^(-1)K^(-1) .thermal conductivity of copper =385 Wm^(-1)K^(-1) .
View SolutionTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is

View Solutionचित्र 11.16 में दर्शाए अनुसार लोहे की किसी छड़ (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) के साथ सिरे से सिरे को मिलाकर डाला गया है | लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों की क्रमशः 373 K तथा 273 K पर स्थापित किया गया है | (i) दोनों छड़ों की संधि पर ताप, (ii) संयुक्त छड़ की तुल्य ऊष्मा चालकता, तथा (iii) संयुक्त छड़ में ऊष्मा प्रवाह की दर के लिए व्यंजक निकालिए तथा परिकलित कीजिए |
View Solutionयदि ¯a=l1¯i+m1¯j+n1¯k और ¯b=l2¯i+m2¯j+n2¯k दो मात्रक सदिश हों तथा इनके बीच का कोण θ हो, तो दर्शाइए कि
cosθ=l1l2+m1m2+n1n2.
View Solutionचित्र में दर्शाए अनुसार लोहे की किसी छड़ (L1=0.1 m ,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2 0.1 m ,A2=0.02m2,K2=109Wm2K−1) के साथ सिरे को मिलाकर ढाला गया है | लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों को क्रमशः 373 K तथा 273 K पर स्थापित किया गया है |
दोनों छड़ो की संधि पर ताप
View Solutionलोहे की किसी छड़ (L1=0.1 m ,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2 0.1 m ,A2=0.02m2,K2=109Wm2K−1) के साथ सिरे को मिलाकर ढाला गया है | लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों को क्रमशः 373 K तथा 273 K पर स्थापित किया गया है |
संयुक्त छड़ की तुल्य ऊष्मा चालकता क्या होगी?
View Solutionलोहे की किसी छड़ (L1=0.1 m ,A1=0.02m2,K1=79Wm−1K−1) को किसी पीतल की छड़ (L2 0.1 m ,A2=0.02m2,K2=109Wm2K−1) के साथ सिरे को मिलाकर ढाला गया है | लोहे की छड़ तथा पीतल की छड़ के स्वतंत्र सिरों को क्रमशः 373 K तथा 273 K पर स्थापित किया गया है |
संयुक्त छड़ में ऊष्मा प्रवाह की दर के लिए व्यंजक निकालिए तथा परिकलित कीजिए |
View Solution¯a=2¯i+5¯j+¯k, ¯b=4¯i+m¯j+n¯kలు నకేఖీయ సదిశలైతే, m, n లను కనుక్కోండి.
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in Fig. 11.16. The free ends of the iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (1) the temperature of the function of the two bars, (11) the equivalent thermal conductivity of the compound bar, and (111) the heat current through the compound bar.
View Solution
