A block whose mass is 1kg is fastened to a spring. The spring has a spring constant of 50Nm−1. The block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.Solution in Gujrati
m=1kg,k=50Nm−1,A=10cm=0.1m,x=5cm=0.05m
Angular frequency of the block executes SHM, ω=√km=√501=7.07rads−1.
Its displacement at any time t is, x(t)=Acosωt=0.1cosωt.
Now if x=5cm=0.05m then 0.05=0.1cosωt
∴0.5=cos(ωt)
∴cos(ωt)=12
∴sinωt=sin(π)3=√32
sinωt=0.866 .........(1)
The velocity of the block at x= 5 cm is, x(t)=Acosωt
∴v=dx(t)dt=d(Acosωt)dt
∴v=−Aωsinωt
=−0.1×7.07×sinωt
=−0.1×7.07×0.866 [From equ. (1)]
=−0.612262=−0.61ms−1
Kinetic energy of the block K=12mv2
=12×1×(−0.61)2
=12×0.3727=0.1864=0.19J
Potential energy of the block U=12kx2
=12×50×(0.05)2=25×0.0025=0.0625J
Total energy of the block at distance x= 5 cm
E=K+U=0.19+0.0625
=0.2525≈0.25J.
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM TEXTUAL EXERCISE)
48 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (ADDITIONAL EXERCISE)
9 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-A (TRY YOURSELF)
64 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
Which of the following examples represent periodic motion?
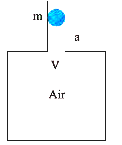
View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionWhat is motion ?
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionA block whose mass is 1 kg is fastened to a spring.The spring has a spring constant 50Nm−1. The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface at t=0. Calculate the kinetic, potential and total energies of the blocak when it is 5cm away from the mean position.
View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 Nm^(-1) . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100N/m. the block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. the kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
View SolutionA block of mass on kg is fastened to a spring with a apring constant 50 Nm^(-1) . The block is pulleed to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Write the expression fr its x (t) and v(t).
View SolutionA block of mass on kg is fastened to a spring with a apring constant 50Nm−1. The block is pulleed to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Write the expression fr its x (t) and v(t).
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 50Nm−1. The block is pulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionless surface from rest at t = 0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the displacement function x(t) for the spring block system?
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 50Nm−1. The block is pulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionless surface from rest at t = 0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 50 N m^(-1) . The block is pulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionless surface from rest at t = 0. Calculate the kinetic, potential and total energies of the block when it is 5 cm away from the mean position.
View SolutionA block whose mass is 1 kg is fastened to a spring.The spring has a spring constant 50Nm^(-1) . The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface at t=0 . Calculate the kinetic, potential and total energies of the block when it is 5cm away from the mean position.
View Solution
