In a p-n junction diode, the current I can be expressed as
I=I0exp(eV2kBT−1)
where I0 is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, kB is the Boltzmann constant (8.6×10−5eV/K) and T is the absolute temperature. If for a given diode I0=5×10−12A and T = 300 K, then
(a) What will be the forward current at a forward voltage of 0.6 V ?
(b) What will be the increase in the current if the voltage across the diode is increased to 0.7 V ?
(c ) What is the dynamic resistance?
(d) What will be the current if reverse bias voltage changes from 1 V to 2 V ? Solution in Gujrati
Current passing through junction diode,
I=I0[exp(eVkBT)−1]
where I0= Reverse saturated current =5×10−12A
T=300K
kB=8.6×10−5eVK−1
=8.6×10−5×1.6×10−19JK−1
=13.76×10−24JK−1,1eV=1.6×10−19JK−1
(a) When V = 0.6 V then
I=I0[exp(eVkBT)−1] ...(1)
but eVkBT=1.6×10−19×0.613.76×10−24×300=0.23255×102
≈23.26
∴ From equation (1),
I1=I0[exp(23.26)−1]A
=5×10−12[exp(23.26)−1]A
=5×10−12[e23.26−1]A
=5×10−12[log(0.4343×23.26)−1]A
=5×10−12[1.2586×1010−1]A
Neglecting 1 compare to 1.2586×1010
=5×10−12×1.2586×1010A
∴I1=0.06293A
(b) When V = 0.7V then
From equation (1),
Taking eVkBT=1.6×10−19×0.713.76×10−24×300=27.13
I2=I0[exp(eVkBT)−1]A
=5×10−12[27.13log(0.4343)−1]A
=5×10−12[6.07×1011−1]A
Neglecting 1 compare to 6.07×1011
=5×10−12×6.07×1011A
∴I2=3.035A
∴ Increase in current ΔI=I2−I1
=3.0350−0.06293
=2.97207A
≈2.972A
(c ) ΔV=0.7−0.6=0.1V
and ΔI=2.972A
∴ Dynamic variable resistance,
rd=ΔVΔI=0.12.972=0.03364Ω
∴rd≈0.0336Ω
(d) When voltage varies from 1 V to 2V then current I0=5×10−12A remains constant it shows that in reverse bias the dynamic resistance is infinite.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS EXERCISE - Section-B : Numericals (Numerical From .DARPAN. Based On Textbook)14videos
SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - KUMAR PRAKASHANCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS EXERCISE - Section-C: NCERT Exemplar Solution (Multiple Choice Qustion (MCQs) )8videos
SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - KUMAR PRAKASHANCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS EXERCISE - Section-B : Numericals (Numerical From Textual illustrations)16videos
SEMICONDUCTOR ELECTRONICS : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - KUMAR PRAKASHANCHAPTER - SAMPLE QUESTION PAPER EXERCISE - PART-B SECTION-C5videos
SAMPLE QUESTION PAPER
- BOOK - KUMAR PRAKASHANCHAPTER - WAVE OPTICSEXERCISE - SECTION-D (MULTIPLCE CHOICE QUESTIONS (MCQS)) (MCQS FROM DARPAN BASED ON TEXTBOOK)239videos
WAVE OPTICS
Similar Questions
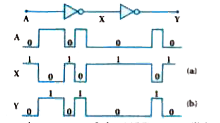
A logic circuit is shown in the diagram. Draw the output signal at the point X and Y for the input signal shown in the figure at point A.
 05:54View Solution
05:54View SolutionThe conductivity of a semiconductor increases with increase in temperature because
05:54View SolutionC, Si and Ge have same lattice structure. Why is C insulator while Si and Ge intrinsic semiconductors?
05:54View SolutionTwo charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/a>>1 .
(c) How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?07:00View SolutionAccording to particle theory of light what is the velocity of light in a dense medium, compared to that in rare medium ?
08:08View SolutionIn a p−n junction diode, the currect I can expressed as I=I0exp(eV2kBT−1) where I0 is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, KB is the Boltzmann constant (8.6×10−5eV/K) and T is the absolute temperature. If for a given diode Io=5×10−12A and T=300K, then
(a) What will be the forward current at a formward voltage of 0.6V ?
(b) What will be the increase in the current if the voltage across the diode is increased to 0.7V ?
( c) What is the dynamic resistance ?
(d) What will be current if reverse bias voltage changes from 1V to 2V ?View SolutionIn a p−n junction diode, the currect I can expressed as I=I0exp(eV2kBT−1) where I0 is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, KB is the Boltzmann constant (8.6×10−5eV/K) and T is the absolute temperature. If for a given diode Io=5×10−12A and T=300K, then
(a) What will be the forward current at a formward voltage of 0.6V ?
(b) What will be the increase in the current if the voltage across the diode is increased to 0.7V ?
( c) What is the dynamic resistance ?
(d) What will be current if reverse bias voltage changes from 1V to 2V ?01:43View SolutionIn a p−n junction diode, the currect I can expressed as I=I0exp(eV2kBT−1) where I0 is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, KB is the Boltzmann constant (8.6×10−5eV/K) and T is the absolute temperature. If for a given diode Io=5×10−12A and T=300K, then
(a) What will be the forward current at a formward voltage of 0.6V ?
(b) What will be the increase in the current if the voltage across the diode is increased to 0.7V ?
( c) What is the dynamic resistance ?
(d) What will be current if reverse bias voltage changes from 1V to 2V ?06:51View Solutionकिसी p-n संधि डायोड में धारा को इस प्रकार व्यक्त किया जा सकता है-
I=I0[exp(eVkBT)−1] जहाँ I0 को उत्क्रमित संतृप्त धारा कहते हैं, V डायोड के सिरों पर वोल्टता है तथा यह अग्रदिशिक बायस के लिए धनात्मक तथा पश्चदिशिक बायस के लिए ऋणात्मक है। I डायोड से प्रवाहित धारा kB है बोल्ट्जमैन नियतांक (8.6×10−5eV/K) है तथा T परम ताप है। यदि किसी दिए गए डायोड के लिए I0=5×10−12 A तथा T = 300K है, तब 0.6V अग्रदिशिक वोल्टता के लिए अग्रदिशिक धारा क्या होगी?View Solutionकिसी p-n संधि डायोड में धारा को इस प्रकार व्यक्त किया जा सकता है-
I=I0[exp(eVkBT)−1] जहाँ I0 को उत्क्रमित संतृप्त धारा कहते हैं, V डायोड के सिरों पर वोल्टता है तथा यह अग्रदिशिक बायस के लिए धनात्मक तथा पश्चदिशिक बायस के लिए ऋणात्मक है। I डायोड से प्रवाहित धारा kB है बोल्ट्जमैन नियतांक (8.6×10−5eV/K) है तथा T परम ताप है। यदि किसी दिए गए डायोड के लिए I0=5×10−12 A तथा T = 300K है, तब यदि डायोड के सिरों पर वोल्टता को बढ़ाकर 0.7V कर दें तो धारा में कितनी वृद्धि हो जाएगी ?View SolutionIn a p-n junction diode, the currentI can be expressed as I=I_(0) exp ((eV)/(2K_(B)T)-1) where I_(0) is called the reverse saturation current,V is the voltage across the diode andis positive for forward bias and negative for reverse biase,and I is the current through the diode, k_(B) is the Boltzmann constant ( 8.6 xx10^(-5) eV//K) and T is the absolute temperature . If fora given diode I_(0)=5 xx10^(-12) A and T = 300K , then (i) What will be the forward current at a forward voltage of 0.6V? (b) What will be the increase in the current if the voltage across the diode is increased to 0.7 V ? (c ) What is the dynamic resistance ? (d) What will be the current if reverse biase voltage changes from 1V to 2V ?
05:59View SolutionPassage II Diode current in a p-n junction diode is given by I-I_(0)[exp(eV)/(2kT)-1] where I_(0) is the reverse saturation current V is the voltage across the diode k is the boltzmann constant and T is the abosolute temperatuer For a given diode I_(0)=5 pA and T =300 k When the reverse bias voltage bias voltage changes from 1 v to 2 V the current will become equal to
06:41View SolutionIn a p-n junction diode, the current I can be expressed as I= I_(0) "exp" ((eV)/(k_(B)T)-1) where I_(0) is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, k_(B) is the Boltzmann constant (8.6 xx 10^(–5) eV//K) and T is the absolute temperature. If for a given diode I_(0) = 5 xx 10^(-12) A and T = 300 K, then (a) What will be the forward current at a forward voltage of 0.6 V? (b) What will be the increase in the current if the voltage across the diode is increased to 0.7 V? (c) What is the dynamic resistance? (d) What will be the current if reverse bias voltage changes from 1 V to 2 V?
03:32View SolutionIn a p-n junction diode, the current I can be expressed as
I=I0exp(eV2kBT−1)
where I0 is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, kB is the Boltzmann constant (8.6×10–5eV/K) and T is the absolute temperature. If for a given diode I0=5×10−12 A and T = 300 K, then
(a) What will be the forward current at a forward voltage of 0.6 V?
(b) What will be the increase in the current if the voltage across the diode is increased to 0.7 V?
(c) What is the dynamic resistance?
(d) What will be the current if reverse bias voltage changes from 1 V to 2 V?02:07View SolutionIn a p-n junction diode, the current I can be expressed as
I=I0exp(eV2kBT−1)
where I0 is called the reverse saturation current, V is the voltage across the diode and is positive for forward bias and negative for reverse bias, and I is the current through the diode, kB is the Boltzmann constant (8.6×10–5eV/K) and T is the absolute temperature. If for a given diode I0=5×10−12 A and T = 300 K, then
(a) What will be the forward current at a forward voltage of 0.6 V?
(b) What will be the increase in the current if the voltage across the diode is increased to 0.7 V?
(c) What is the dynamic resistance?
(d) What will be the current if reverse bias voltage changes from 1 V to 2 V?07:00View Solution

