A crate of mass 'm' is placed on a plank which moves with an acceleration a. The minimum value of m(ug-a) tension T required to slide the crate on the plnak is m(μg−a)√μ2+n where n is.
The correct Answer is:1
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - PRACTICE SHEET EXERCISE-II)(LEVEL-I) (STRAIGHT OBJECTIVE TYPE QUESTIONS)3videos
FRICTION
- BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - PRACTICE SHEET EXERCISE-II)(LEVEL-II) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)1videos
FRICTION
- BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - PRACTICE SHEET (EXERCISE-I) (LEVEL-II) (STRAIGHT OBJECTIVE TYPE QUESTIONS)6videos
FRICTION
- BOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Questions for Descriptive Answers14videos
FLUID MECHANICS
- BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)12videos
GAUSS.S LAW
Similar Questions
A body of mass M is moving in +x-direction with acceleration a. Find the minimum value of μ so that a body of mass m can be held stationary with respect to M, on the vertical side of M.
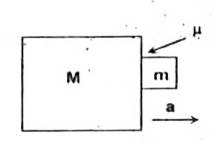 View Solution
View SolutionA body of mass M is moving in +x-direction with acceleration a. Find the minimum value of μ so that a body of mass m can be held stationary with respect to M, on the vertical side of M.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m kg is placed on a plank. The plank is moving with an acceleration 6ˆi+6ˆj (in m/s2 ). The frictional force acting on the block is (μ=0.5,g=10m/s2) :
 A6mB7mC8mD8.5m
A6mB7mC8mD8.5m - Question 2 - Select One
A block of mass m is placed in equilibrium on a moving plank. The maximum horizontal acceleration of the plank for μ=0.2 is:
A2m/s2B3m/s2Cdependent on the mass mDnone of these - Question 3 - Select One or More
Figure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms−2
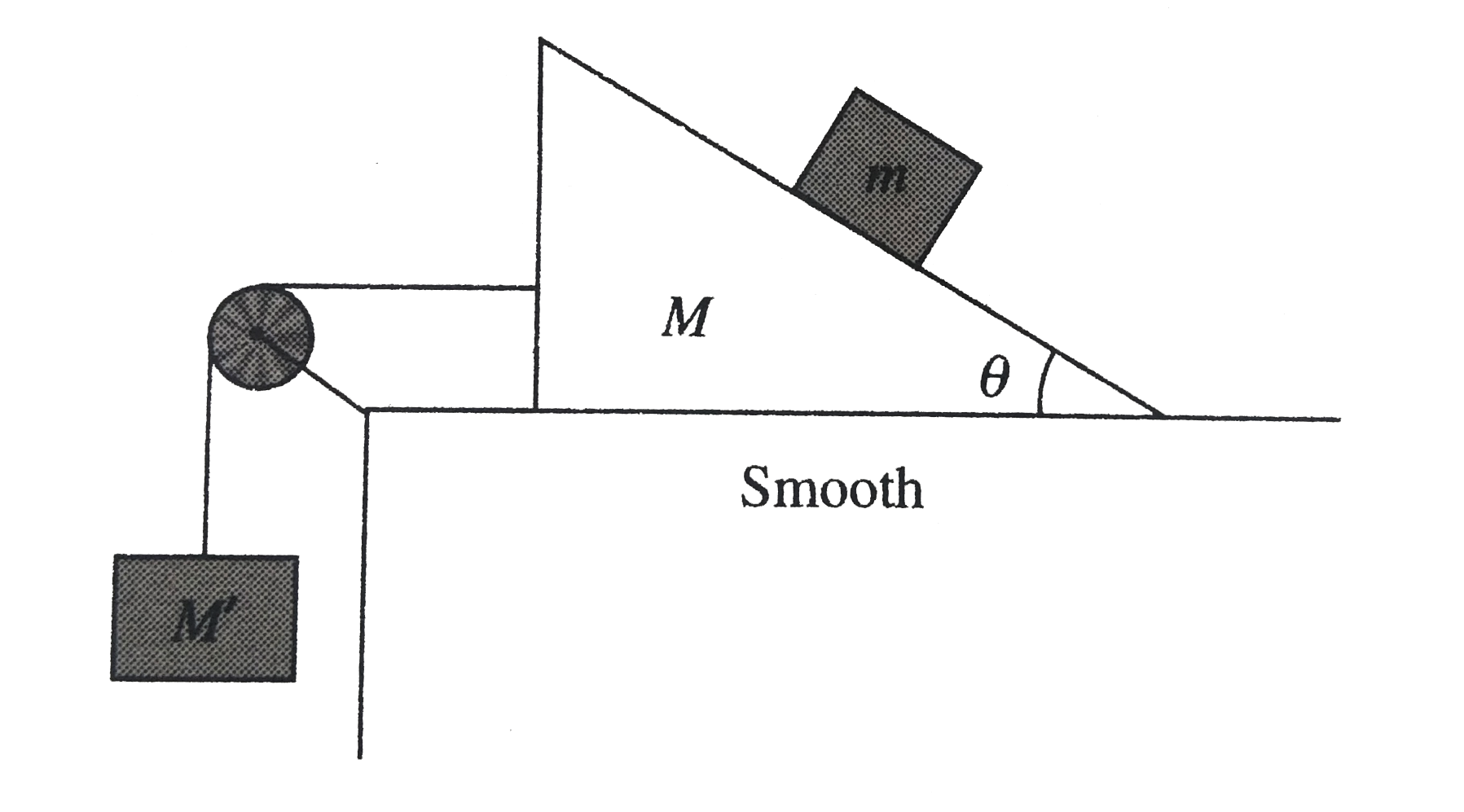 AThe value of M' is Mcotθ1−cotθBThe value of M' is Mtanθ1−tanθCThe value of tension in the string is MgtanθDThe value of tension is Mgcotθ
AThe value of M' is Mcotθ1−cotθBThe value of M' is Mtanθ1−tanθCThe value of tension in the string is MgtanθDThe value of tension is Mgcotθ
A plank of mass m1 with a uniform solid sphere of mass m2 placed on it rests and a force F is applied to the plank. The acceleration of the plank provided there is no sliding between the plank and the sphere is (Fm1+n7m2) then the value of n is
 View Solution
View SolutionFigure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms−2
 View Solution
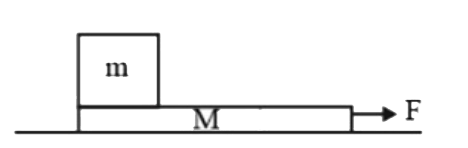
View SolutionA bolck of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
 View Solution
View SolutionA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :
 View Solution
View SolutionA block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
 View Solution
View Solution

