A uniform rod of length 'L' and mass 'M' has been placed on a rough horizontal surface. The horizontal force 'F' applied on the rod such that the rod is just in the state of rest. If the coefficient of friction varies according to the relation μ = kx. Where 'K' is a +ve constant. Then
Tension at mid points is F/3
Tension is mid point is F/4
Tension at x=L4isF16
Tension at x=3L4 is 9F16
The correct Answer is:B, C, D
Topper's Solved these Questions
- FRICTION BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LELVL-II) (LECTURE SHEET (ADVANCED)) (LINKED COMPREHENSION TYPE QUESTIONS)
2 Videos
- FRICTION BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
5 Videos
- FRICTION BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LELVL-I (MAIN)) (STRIAGHT OBJECTIVE TYPE QUESTIONS)
14 Videos
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Questions for Descriptive Answers
14 Videos
- GAUSS.S LAW BOOK - AAKASH SERIESCHAPTER - GAUSS.S LAW EXERCISE - PROBLEMS (LEVEL - II)
12 Videos
Similar Questions
A uniform rod of length L and mass M has been placed on a rough horizontal surface. The horizontal force F applied on the rod is such that the rod is just in the state of rest. If the coefficient of friction varies according to the relation μ =Kx where K is a +ve constant. Then the tension at mid point of rod is?
View SolutionA uniform rod of length L and mass M has been placed on a rough horizontal surface as shown in the figure. The rod is pulled by applying a horizontal force. The coefficient of friction μ between the surface and the rod is given by
μ={μ0x0≤x≤L0x>L, where μ0 is a positive constant. The heat generated due to friction as the rod moves by a distance L is
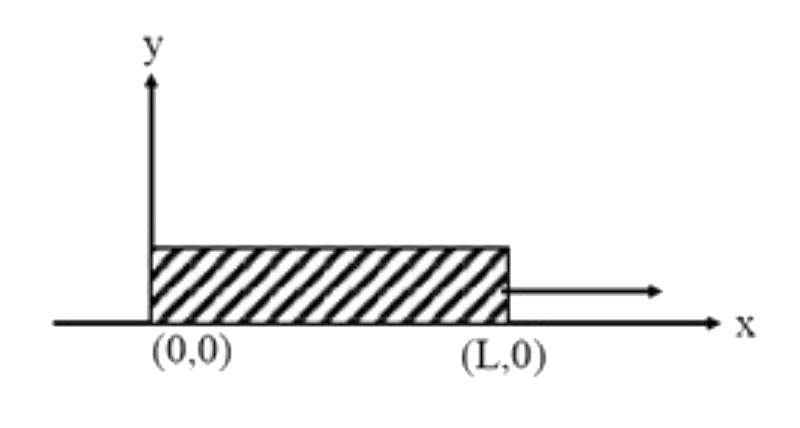
View Solution
Knowledge Check
A rod of length l, mass M, cross section area A is placed on a rough horizonatal surface. A horizonatal force F is applied to rod as shwon in figure. The coefficient of fricition between rod and surface is μ, the Young, modulus of material of rod is Y. [Assume that fricition force is distributed uniformly on rod]
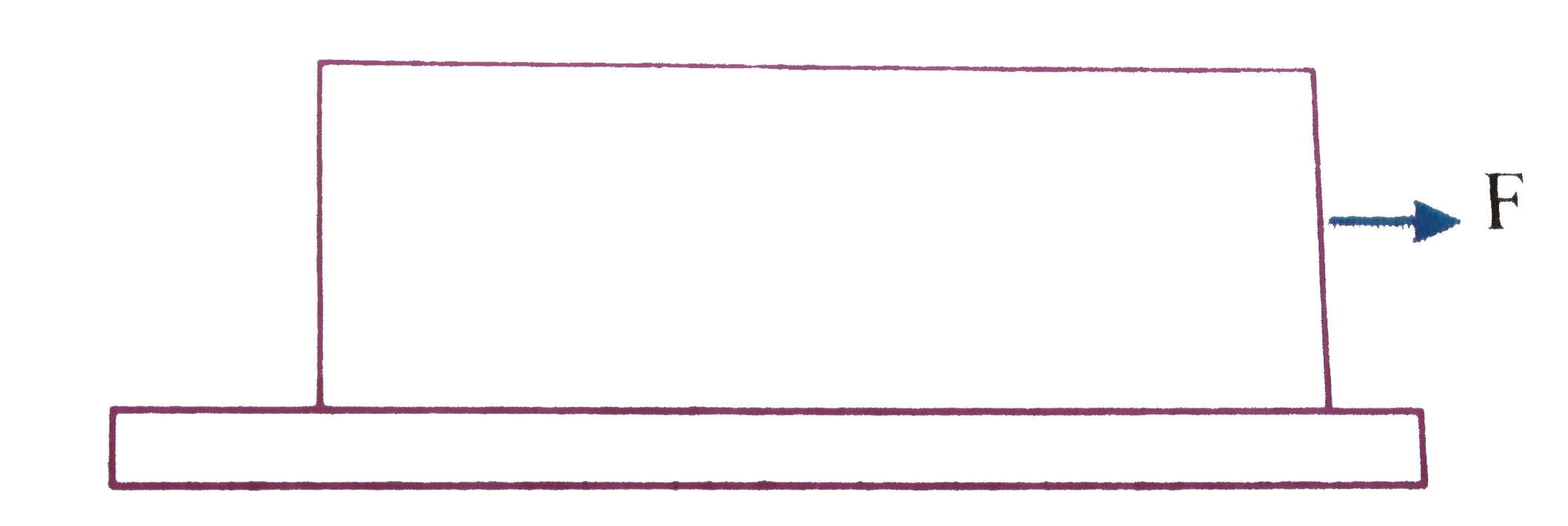
The elongation in the rod if F<μMg isAZeroB⎡⎢⎣F−μMg22AY⎤⎥⎦lCFl2AYDNoneA rod of length l, mass M, cross section area A is placed on a rough horizonatal surface. A horizonatal force F is applied to rod as shwon in figure. The coefficient of fricition between rod and surface is μ, the Young, modulus of material of rod is Y. [Assume that fricition force is distributed uniformly on rod]

Teh elongation in rod if F>μMg isA(F−μMg)l2AYB⎡⎢⎣F−μMg22AY⎤⎥⎦lCFl2AYDNoneA uniform thin rod of length 2L and mass m lies on a horizontal table. A horizontal impulse J is given to the rod at one red. There is no friction. The total kinetic energy of the rod just after the impulse will be
AJ22mBJ2mC2J2mD6J2m
A uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA uniform rod of length L and mass M is pulled horizontally on a smooth surface with a force F. Determine the elongation of rod if Young's modulus of the material is Y.
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
View Solution
