यदि α=Fv2sinβt है α तथा β की विमाऐं ज्ञात करो, जहां v = वेग, F = बल t = समय है।
यहां sin gt ft विमाहीन होते हैं अत: [βt]=1⇒[β]=[1t]=[T−1],[α]=[Fv2sinβt]=[Fv2]=[MLT−2L2T2]=[ML−1]
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - भौतिक जगत, मात्रक एवं विमायें तथा मापन में त्रुटियाँEXERCISE - BEGINNER.S BOX -12videos
भौतिक जगत, मात्रक एवं विमायें तथा मापन में त्रुटियाँ
- BOOK - ALLEN HINDICHAPTER - भौतिक जगत, मात्रक एवं विमायें तथा मापन में त्रुटियाँEXERCISE - BEGINNER.S BOX -24videos
भौतिक जगत, मात्रक एवं विमायें तथा मापन में त्रुटियाँ
- BOOK - ALLEN HINDICHAPTER - प्रत्यावर्ती धाराEXERCISE - EXERCISE-IV (ASSERTION & REASON)19videos
प्रत्यावर्ती धारा
- BOOK - ALLEN HINDICHAPTER - भौतिकी में प्रयुक्त आधारभुत गणित EXERCISE - EXERCISE-IV (ASSERTION AND REASON)11videos
भौतिकी में प्रयुक्त आधारभुत गणित
Similar Questions
MKS पद्धति में गुरूत्वीय नियतांक G का मान 6.67×10−11N−me/kg2 है। CGS पद्धति में इसका मान क्या होगा?
08:37View Solutionनिम्न का मिलान कीजिए।
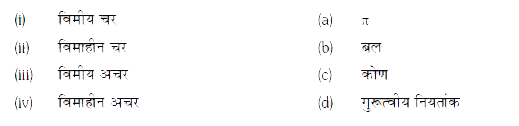 01:34View Solution
01:34View Solutionकथन : आदर्श चोक कुण्डली में शक्ति हानि शून्य है।
कारण : आदर्श चोक कुण्डली का प्रतिरोध शून्य होता है।06:49View Solutionकथनः यदि प्रांरभिक व अंतिम स्थितियां संपाती होती है तो विस्थापन शून्य सदिश होता है।
कारणः कोई भौतिक राशि सदिश नहीं कहला सकती है यदि उसका परिमाण शून्य हो।04:47View SolutionIf the function f:[0,8]→R is differentiable, then for 0<α<1<β<2,∫80f(t)dt is equal to (a) 3[α3f(α2)+β2f(β2)] (b) 3[α3f(α)+β2f(β)] (c) 3[α3f(α2)+β2f(β3)] (d) 3[α2f(α3)+β2f(β3)]
03:11View SolutionIf alpha and beta are the zeroes of the quadratic polynomial f(t)=t^(2)-4t+3, then the value of alpha^(4)beta^(3)+alpha^(3)beta^(4) is
05:29View Solution(a) The displacement s of a particale in time t related as s = alpha + beta t + gamma t^(2) + delta t^(2) (b) The veloctiy v of particle varies with time as v = alpha t + beta t^(2) + (gamma )/(t + s) Findk the dimension fo alpha, beta, gamma and delta .
05:00View SolutionThe function f is given by f=Asinαx+Bcosβt, where x is displacement and t is the time. The dimensions of α/β is
04:55View SolutionIf α=Fv2sinβt, find dimensions of α and β. Here v=velocity, F= force and t= time.
02:16View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
01:32View Solutionयदि द्विघाती समीकरण, x2+xsinθ−2sinθ=0,θ∈(0,π2), के मूल α तथा β हैं , तो α12+β12(α−12+β−12).(α−β)24 बराबर है
05:58View Solutionयदि α=(λ−2)a+b तथा β=(4λ−2)a+3b दो दिए गए सदिश है, जहाँ सदिश a तथा b सरीख नहीं है । λ का वह मान जिसके लिए α तथा β सरीख है, है
04:28View SolutionIf sin ( alpha - beta) = 1/2 " तथा " cos ( alpha + beta) = 1/2 " जहां " alpha , beta If the positive angle is alpha " और " beta Find the value of
02:07View SolutionIf αandβ are zeros of f(t)=t2−4t+3, find the value of α4β3+β4α3 .
01:59View Solution

