शुद्ध सिलिकॉन में 300 K ताप पर 1.5×1016m−3 की समान इलेक्ट्रॉन ( ne) औ (nh) सान्द्रता है (nh) का मान बढ़कर 3×1022मी−3 हो जाता है Si में ne की गणना करों।
तापीय साम्यावस्था में किसी अपमिश्रित अर्द्धचालक के लिये n(e)nh=n(i)2 द्र(व्यमानुपाती क्रिया के नियम से)
ne=n2inh=(1.5×1016)23×1022=7.5×109m−3
Topper's Solved these Questions
- अर्द्धचालक तथा अंकीय इलेक्ट्रॉनिक्स BOOK - ALLEN HINDICHAPTER - अर्द्धचालक तथा अंकीय इलेक्ट्रॉनिक्स EXERCISE - BEGINNER.S BOX-1
4 Videos
- अर्द्धचालक तथा अंकीय इलेक्ट्रॉनिक्स BOOK - ALLEN HINDICHAPTER - अर्द्धचालक तथा अंकीय इलेक्ट्रॉनिक्स EXERCISE - BEGINNER.S BOX-2
8 Videos
- ऊष्मीय भौतिकी BOOK - ALLEN HINDICHAPTER - ऊष्मीय भौतिकी EXERCISE - EXERCISE-IV Assertion & Reason
63 Videos
Similar Questions
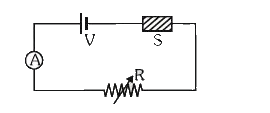
चित्र में प्रदर्शित S परिवर्तित प्रतिरोध R औ V वोल्टता के स्रोत के साथ श्रेणीक्रम में जुड़ा हुआ है (A ) के पाठ्यांक को नियत रखने के लिए आप R के मान को बढ़ाएंगे या घटाएंगे ?
View Solutionबिना अभिनति वाली p-n संधि पर 0.2 वोल्ट विभव प्राचीर विद्यमान है किसी होल को p-ओर से n-ओर विसरित होने के लिये न्यूनतम कितनी गतिज ऊर्जा की आवश्यकता होगी, यदि
संधि अभिनत नहीं है
View Solutionकथन : द्रवों में सामान्यतया ठोसों की तुलना में अधिक प्रसार होता है।
कारण : द्रवों में अन्तराण्विक बल ठोसों की तुलना में कमजोर होते है।
View SolutionPure Si at 500K has equal number of electron (ne) and hole (nh) concentration of 1.5×1016m−3. Dopping by indium. Increases nh to 4.5×1022m−3. The doped semiconductor is of
View SolutionPure Si at 300 K has equal electron (n_(e)) and hole (n_(h)) concentrastions of 1.5xx10^(16)m^(-3) doping by indium increases n_(h) to 4.5xx10^(22)m^(-3) . Caculate n_(theta) in the doped Si-
View Solutionकिसी नैज अर्धचालक में ऊर्जा अंतराल Eg का मान 1.2eV है। इसकी होल गतिशीलता इलेक्ट्रॉन की गतिशीलता की तुलना में काफी कम है तथा ताप पर निर्भर नहीं है। इसकी 600K तथा 300K पर चालकताओं का क्या अनुपात है? यह मानिए कि नैज वाहक सांद्रता ni की ताप निर्भरता इस प्रकार व्यक्त होती है-
ni=n0 exp (Eg2kBT)
जहां n0 एक स्थिरांक है।
View SolutionPure Si at 300 K has equal electron (n_e) and hole (n_(h)) concentration of 2.xx10^(16) per m^(3) . Doping by indium increases n_(h) to 4xx10^(22) per m^(3) . Calculate n_(e) in the doped silicon.
View SolutionPure Si at 500 K has equal number of electron ( n_(e)) and hole ( n_(h)) concentrations of 1.5 xx10^(16) "m"^(-3) . Doping by indium increases n_(h) to 4.5 xx10^(22) "m" ^(-3) . The doped semiconductor is of
View SolutionPure Si at 300 K has equal electron (ne) and hole (nh) concentrations of 1.5×1016m−3 doping by indium increases nh to 4.5×1022m−3. Caculate ne in the doped Si-
View SolutionPure Si at 300 K has equal electron (ne) and hole (nh) concentrations of 1.5×1016m−3 doping by indium increases nh to 4.5×1022m−3. Caculate ne in the doped Si-
View SolutionPure Si at 300 K has equal electron (ne) and hole (nh) concentration of 2.×1016 per m3. Doping by indium increases nh to 4×1022 per m3. Calculate ne in the doped silicon.
View Solution300 K पर शुद्ध सिलिकॉन में समान इलेक्ट्रॉन (ne) तथा कोटर (nh) की सान्द्रता 1.5×1016 मी−3 है। इन्डियम के अपमिश्रण पर nh बढ़कर
4.5×1022 मी−3 हो जाती हैं, अपमिश्रित सिलिकॉन में ne है
View SolutionPure Si at 300 K has equal electron (ne) and hole (nh) concentration of 1.5×1016m−3 . Doping by indium increases nh to 4.5×1022m−3 . Calculate ne in the doped silicon.
View SolutionPure Si at 300 K has equal electron (ne) and hole (nh) concentration of 1.5×1016m6(−3). Doping by indium increases into 4.5×1022m−3. Calculate ne in the doped silicon .
View SolutionPure Si at 500K has equal number of electron (n_(e)) and hole (n_(h)) concentration of 1.5xx10^(16)m^(-3) . Dopping by indium. Increases n_(h) to 4.5xx10^(22) m^(-3) . The doped semiconductor is of
View Solution
