Conductivity k, is equal to ......
1RlA
G⋅R
Λm
lA
To solve the question regarding the expression for conductivity (Kappa, κ), we can follow these steps:
1. Understanding Conductivity (Kappa, κ):
- Conductivity, denoted by the symbol κ (kappa), is a measure of a solution's ability to conduct electricity. It indicates how well electric current can pass through a particular electrolyte solution.
Hint: Remember that conductivity is related to the movement of ions in a solution.
2. Relationship with Resistivity:
- Conductivity is the inverse of resistivity. This means that if a solution has high conductivity, it has low resistivity, and vice versa. The relationship can be expressed mathematically as:
κ=1ρ
where ρ (rho) is the resistivity of the solution.
Hint: Think of resistivity as the opposition to the flow of electric current.
3. Expression for Conductivity:
- The expression for resistivity in terms of resistance (R), length (L), and cross-sectional area (A) of the conductor is given by:
R=ρLA
- Rearranging this equation gives us:
ρ=RAL
- Substituting this back into the equation for conductivity gives:
κ=1ρ=AR⋅L
Hint: Remember that conductance (G) is defined as the reciprocal of resistance (G = 1/R).
4. Final Expression:
- Therefore, the final expression for conductivity can be summarized as:
κ=AR⋅L
- This shows that conductivity depends on the area of cross-section of the conductor, the resistance, and the length of the conductor.
Hint: Consider how changes in area or length affect the conductivity of a solution.
Summary:
Conductivity (κ) is equal to AR⋅L, where A is the cross-sectional area, R is the resistance, and L is the length of the conductor. It is a measure of how well a solution can conduct electric current, being inversely related to resistivity.
- Conductivity, denoted by the symbol κ (kappa), is a measure of a solution's ability to conduct electricity. It indicates how well electric current can pass through a particular electrolyte solution.
- Conductivity is the inverse of resistivity. This means that if a solution has high conductivity, it has low resistivity, and vice versa. The relationship can be expressed mathematically as:
κ=1ρ
where ρ (rho) is the resistivity of the solution.
- The expression for resistivity in terms of resistance (R), length (L), and cross-sectional area (A) of the conductor is given by:
R=ρLA
- Rearranging this equation gives us:
ρ=RAL
- Substituting this back into the equation for conductivity gives:
κ=1ρ=AR⋅L
- Therefore, the final expression for conductivity can be summarized as:
κ=AR⋅L
- This shows that conductivity depends on the area of cross-section of the conductor, the resistance, and the length of the conductor.
Conductivity (κ) is equal to AR⋅L, where A is the cross-sectional area, R is the resistance, and L is the length of the conductor. It is a measure of how well a solution can conduct electric current, being inversely related to resistivity.
Topper's Solved these Questions
- D AND F-BLOCK ELEMENTSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - D AND F-BLOCK ELEMENTSEXERCISE - Short Answer Type Question
20 Videos
- GENERAL PRINCIPLE AND PROCESSES OF ISOLATION OF ELEMENTS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GENERAL PRINCIPLE AND PROCESSES OF ISOLATION OF ELEMENTS EXERCISE - Long Answer Type Questions
1 Videos
Similar Questions
The conductance of a solution of an electrolyte is equal to that of its specific conductance The cell constant of the conductivity cell is equal to
View SolutionA conductivity cell is used to measure the conductance of electrolyte . It makes use of conductivity of water which does not contain any ions. The cell constant of conductivity cell is determined.
If the cell constant is 0.40cm−1, the conductivity of 0.051MNaCl solution having R=1850ohm is equal to
View Solution
Knowledge Check
Michaelis Menten Constant (Km) is equal to
Athe rate of reactionBthe rate of enzymatic activityCsubstrate concentration at which the reaction attains half of its maximum velocityDsubstrate concentration at which the rate of reaction is maximum.IF two metallic plates of equal thickness and thermal conductivities K1andK2 are put together face to face anda common plate is constructed, then the equivalent thermal conductivity of this plate will be
AK1K2K1+K2B2K1K2K1+K2C(K21_K22)3/2K1K2D(K21+K22)3/22K1K2
Three rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View SolutionTwo bar of identical dimensions are kept as shown in figure. If K1 and K2are their coefficients of thermal conductivities, then equivalent K
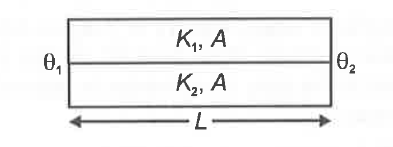
View SolutionThermal conductivity of inner core of radius r is K and of the outer one of radius 2r is 2K. Find equivalent value of thermal conductivity between its two ends.
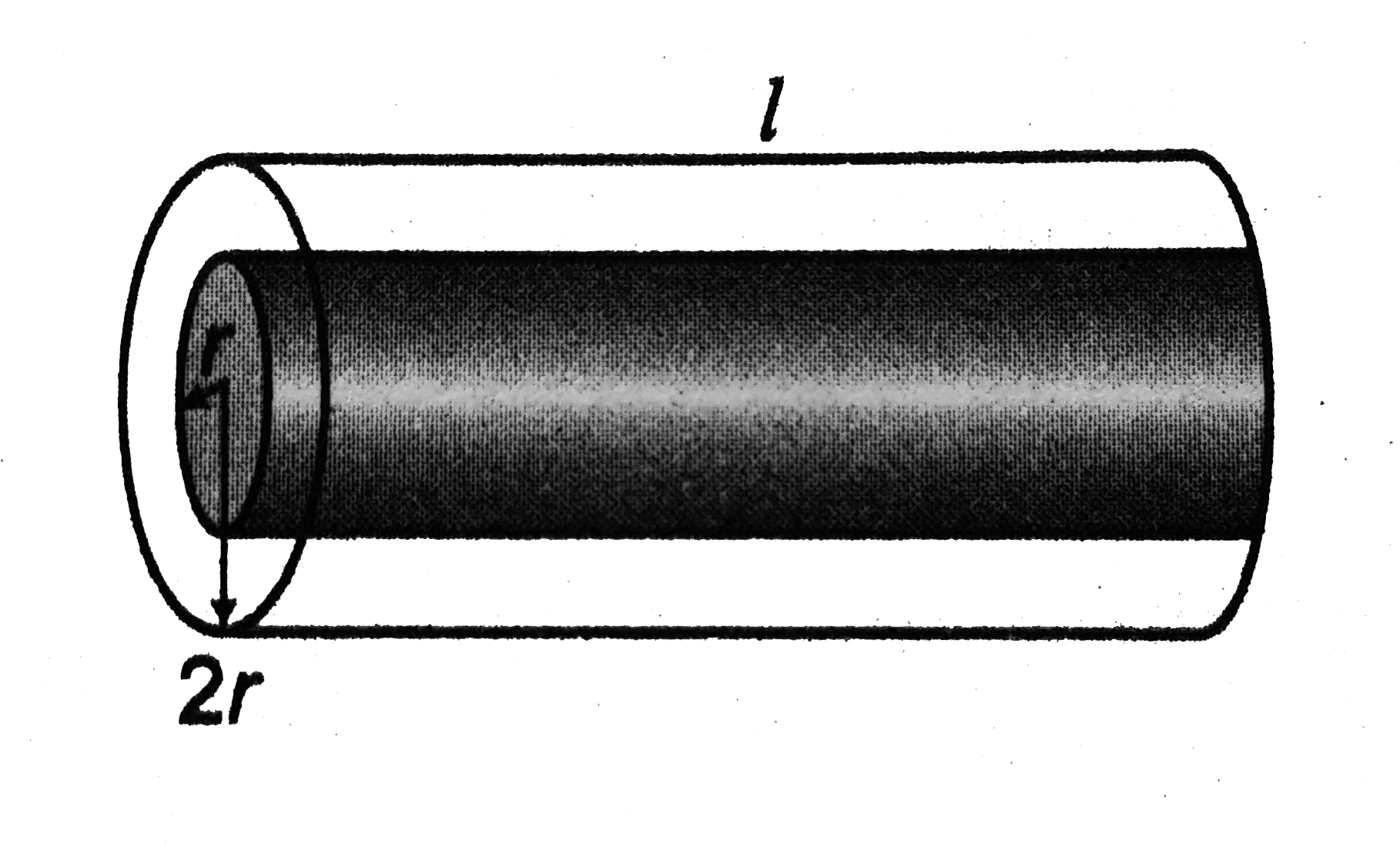
View SolutionSteady state temperature are shown in the diagram. Find ratio of thermal conductivity k1k2 if length of all rods are same
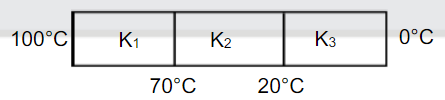
View SolutionBy diluting a weak electrolyte, specific conductivity (Kc) and equivalent conductivity (λc) change as -
View SolutionBy diluting a weak electrolyte, specific conductivity (Kc) and equivalent conductivity (λc) change as
View Solution
