A car starts from rest and moves along the x-axis with constant acceleration 5ms−2 for 8 seconds. If it then continues with constant velocity, what distance will the car cover in 12 seconds since it started from the rest ?
Given, the car starts from rest so its initial velocity u = 0
Acceleration, (a)= 5ms−2 and time (t) = 8s
From first equation of motion,
v = u + at
On putting a = 5ms−2 and t = 8 s in above equation, we gel
v=0+5×8=40ms−1
So, final velocity v is 40ms−1 .
Again, from second equation of motion.
s = ut +12at2
On putting t = 8s and a = 5ms−2 in above equation we get
s=0×8+12×5×(8)2=12×5×64=5×32=160m
So, the distance covered in 8 s is 160m.
Given, total time t = 12s.
After 8s, the car continues with constant velocity i.e., the car will move with a velocity of 40ms−1
So, ramaining time t' = 12s−8s=4s
The distance covered in the last 4s(s) = Velocity × Time [∵ Distance = Velocity × Time]
= 40×4 = 160m
[We have used the direct formual because after 8s, car is moving with constant velocity i.e., zero acceleration]
∴ Total distance travelled in 12 s from the start
D = s+s=160+160=320m
Topper's Solved these Questions
- MOTIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTIONEXERCISE - Long Answer Type Questions
6 Videos
- MOTIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MOTIONEXERCISE - Long Answer Type Questions
6 Videos
- GRAVITATIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - GRAVITATIONEXERCISE - LONG ANSWER TYPE QUESTIONS
4 Videos
- SOUNDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SOUNDEXERCISE - Long Answer Type Questions
3 Videos
Similar Questions
A car starts from rest and moves with uniform acceleration of 5 m/s2 for 8 sec. If the acceleration ceases after 8 seconds then find the distance covered in 12s starting from rest.
View SolutionA particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View Solution
Knowledge Check
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A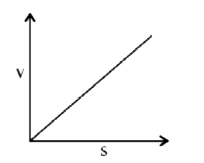 B
B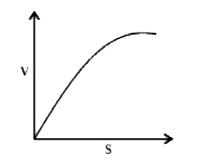 C
C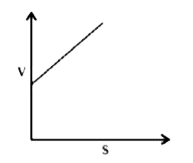 D
D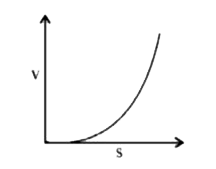
A car starts from rest and moves with constant acceleration. In first t seconds it covers distance x. Then distance covered by it in next t seconds will be:-
AxB2 xC3 xD4 xA car starts from rest and accelerates at a constant rate in a straight line. In the first second, the car covers a distance of 2.0 meters. How much additional distance will the car cover during the second second of its motion ?
A2.0 mB6.0 mC4.0 mD8.0 m
A car starts from rest and moves with uniform acceleration of 5m/s^(2 for 8sec .If the acceleration ceases after 8seconds then find the distance covered in 12s starting from rest (in metres)
View SolutionA body starts from rest and moves with uniform acceleration of 5ms−2 for 8 seconds. From that time the acceleration ceases. Find the distance covered in 12s starting from rest.
View SolutionA car starts from rest and moves with uniform acceleration of "5m/s^(2)for 8 sec.If theacceleration ceases after 8 seconds then find the distance covered in 12 s starting from rest (in metres)
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View Solution
