If the coordinates of the two points are P(-2,3) and Q(-3,5) , then (Abscissa of P)-(Abscissa of Q) is
The correct Answer is:B
To solve the problem, we need to find the difference between the abscissa (x-coordinate) of point P and the abscissa of point Q. Here’s a step-by-step solution:
Step 1: Identify the coordinates of points P and Q.
- The coordinates of point P are given as P(-2, 3).
- The coordinates of point Q are given as Q(-3, 5).
Step 2: Determine the abscissa of point P.
- The abscissa of point P is the x-coordinate of P.
- From the coordinates P(-2, 3), the abscissa of P is -2.
Step 3: Determine the abscissa of point Q.
- The abscissa of point Q is the x-coordinate of Q.
- From the coordinates Q(-3, 5), the abscissa of Q is -3.
Step 4: Calculate the difference between the abscissas.
- We need to find (Abscissa of P) - (Abscissa of Q).
- This translates to: -2 - (-3).
Step 5: Simplify the expression.
- When subtracting a negative number, it is equivalent to adding its positive counterpart.
- So, -2 - (-3) = -2 + 3.
Step 6: Perform the calculation.
- Now, calculate -2 + 3, which equals 1.
Final Answer:
- Therefore, (Abscissa of P) - (Abscissa of Q) = 1.
---
- The coordinates of point P are given as P(-2, 3).
- The coordinates of point Q are given as Q(-3, 5).
- The abscissa of point P is the x-coordinate of P.
- From the coordinates P(-2, 3), the abscissa of P is -2.
- The abscissa of point Q is the x-coordinate of Q.
- From the coordinates Q(-3, 5), the abscissa of Q is -3.
- We need to find (Abscissa of P) - (Abscissa of Q).
- This translates to: -2 - (-3).
- When subtracting a negative number, it is equivalent to adding its positive counterpart.
- So, -2 - (-3) = -2 + 3.
- Now, calculate -2 + 3, which equals 1.
- Therefore, (Abscissa of P) - (Abscissa of Q) = 1.
Topper's Solved these Questions
- COORDINATE GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.2 Very Short Answer Type Questions
1 Videos
- COORDINATE GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.3 Short Answer Type Questions
12 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
- HERON'S FORMULABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Long Answer Type Questions
8 Videos
Similar Questions
In figure LM is a line parallel to the Y-axis at a distance of 3 units .
(i) What are the coordinates of the points P,R and Q ?
(ii) What is the difference between the abscissa of the points L and M ?
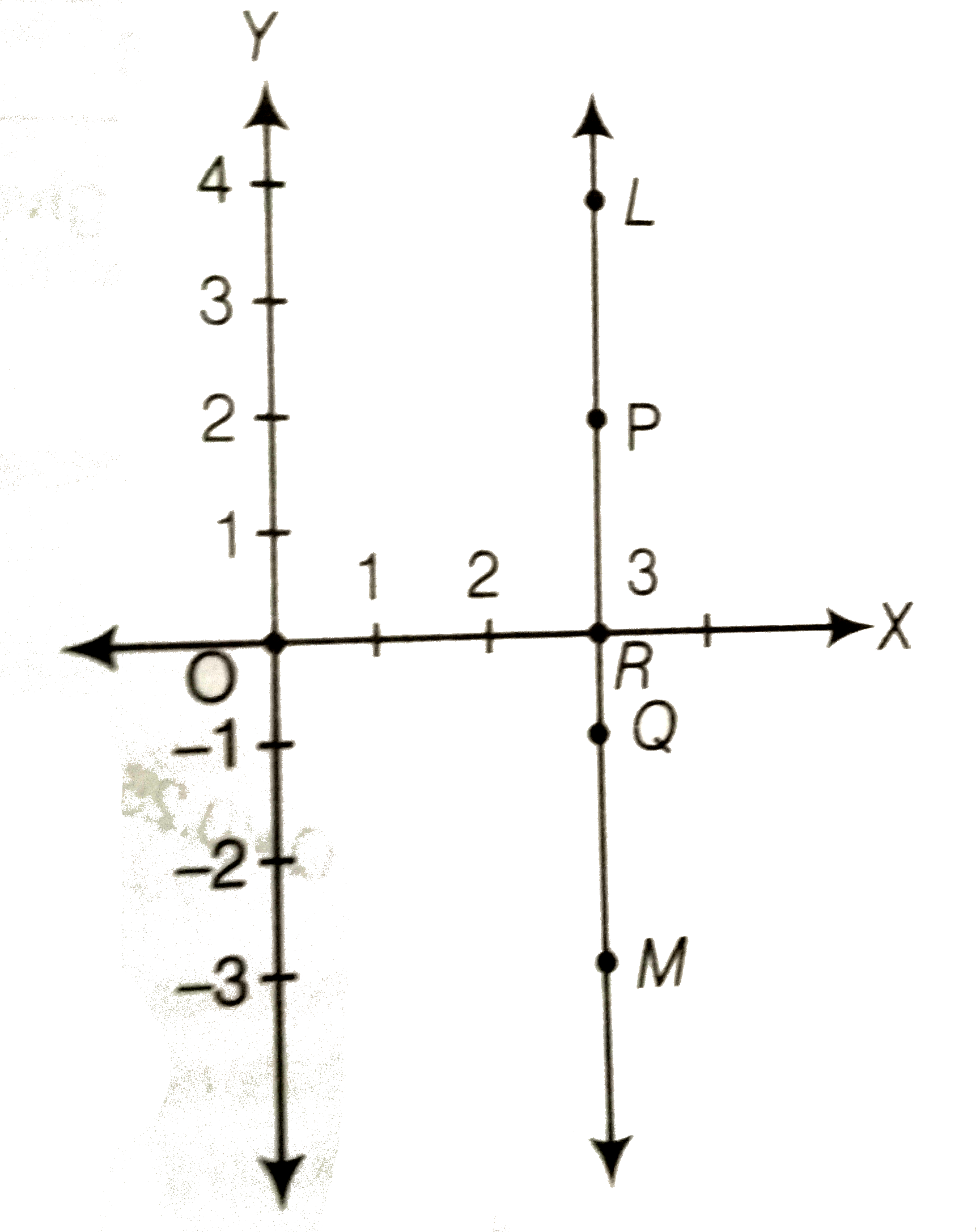
View SolutionThe coordinates of the point P are (−3, 2) . Find the coordinates of the point Q which lies on the line joining P and origin such that OP=OQ .
View SolutionFind the coordinates of points lying on the line joining P(3,−4) and Q(−2,5) that is twice as far from P as Q
View SolutionUse the graph given along side, to find the co ordinates of the point (s) satisfying the given conditions:
(i) The abscissa is 2 (ii) The ordinate is 0 (iii) The ordinate is 3 (iv) The ordinate is 2 (v) The abscissa is 5 (vi) The abscissa is equal to the ordinate (vii) The ordinate is half of the abscissa

View SolutionIf the image of the point (-4, 3, -5) in XZ-plane is
Q then the coordinates of Q is
View SolutionIf the point (p,q) lies on the line joining the points (−4,5) and (−5,7), then show that 2p+q+3=0.
View SolutionIf y1,y2 are the ordinates of two points P and Q on the parabola and y3 is the ordinate of the intersection of tangents at P and Q, then
View SolutionFind the coordinates of the point R on the line segment joining the points P(-1,3) and Q (2,5) such that PR =35 PQ.
View SolutionIf P (a3,4) is the mid - point of the line segment joining the points Q(-6,5) and R(-2,3), then the value of a is
View SolutionThe line segment joining the points (3, −4) and (1, 2) is trisected at the points P and Q . If the coordinates of P and Q are (p, −2) and (5/3, q) respectively. Find the values of p and q .
View Solution
