Consider that an idela gas (n mole) is espanding in a process gives by p=f(v), which passes throught a point (V0,p0). Shown that the gas is absorbing heat at (p0,v0) if the slope of the curve p=f(v) is large than the slope of the adabatic passing throught (p0,v0).
To solve the problem, we need to show that an ideal gas is absorbing heat at the point (P0,V0) if the slope of the curve p=f(v) is greater than the slope of the adiabatic process passing through the same point. We will use the first law of thermodynamics and the definitions of the slopes involved.
1. Identify the Slope of the Given Process:
The process is defined by the equation p=f(v). At the point (P0,V0), the slope of this curve is given by:
dpdv=f′(V0)
2. Identify the Slope of the Adiabatic Process:
For an adiabatic process, the relationship between pressure and volume can be expressed as:
PVγ=constant
The slope of the adiabatic process at the point (P0,V0) can be derived as:
dpdv=−γP0V0
3. Condition for Heat Absorption:
According to the first law of thermodynamics, the change in heat dQ can be expressed as:
dQ=dU+dW
where dU=nCvdT and dW=pdV. Thus, we can write:
dQ=nCvdT+pdV
4. Express Temperature in Terms of Pressure and Volume:
From the ideal gas law, we have:
PV=nRT⟹T=PVnR
Differentiating this gives:
dT=1nR(pdV+Vdp)
5. Substituting dT into the First Law:
Substitute dT into the expression for dQ:
dQ=nCv(1nR(pdV+Vdp))+pdV
Simplifying this, we find:
dQ=CvR(pdV+Vdp)+pdV
6. Finding the Expression for dQdV:
Now, we can express dQdV at the point (P0,V0):
dQdV=CvR(p+VdpdV)+p
7. Condition for Heat Absorption:
For the gas to absorb heat, we need:
dQdV>0
This leads to the condition:
CvR(p+Vf′(V0))+p>0
8. Substituting Values:
At the point (P0,V0), substituting p=P0 and V=V0:
CvR(P0+V0f′(V0))+P0>0
9. Rearranging the Terms:
Rearranging gives:
CvRV0f′(V0)+(1+CvR)P0>0
10. Final Condition:
This implies that:
f′(V0)>−γP0V0
Thus, if f′(V0) (the slope of the curve) is greater than −γP0V0 (the slope of the adiabatic process), the gas is absorbing heat at the point (P0,V0).
The process is defined by the equation p=f(v). At the point (P0,V0), the slope of this curve is given by:
dpdv=f′(V0)
For an adiabatic process, the relationship between pressure and volume can be expressed as:
PVγ=constant
The slope of the adiabatic process at the point (P0,V0) can be derived as:
dpdv=−γP0V0
According to the first law of thermodynamics, the change in heat dQ can be expressed as:
dQ=dU+dW
where dU=nCvdT and dW=pdV. Thus, we can write:
dQ=nCvdT+pdV
From the ideal gas law, we have:
PV=nRT⟹T=PVnR
Differentiating this gives:
dT=1nR(pdV+Vdp)
Substitute dT into the expression for dQ:
dQ=nCv(1nR(pdV+Vdp))+pdV
Simplifying this, we find:
dQ=CvR(pdV+Vdp)+pdV
Now, we can express dQdV at the point (P0,V0):
dQdV=CvR(p+VdpdV)+p
For the gas to absorb heat, we need:
dQdV>0
This leads to the condition:
CvR(p+Vf′(V0))+p>0
At the point (P0,V0), substituting p=P0 and V=V0:
CvR(P0+V0f′(V0))+P0>0
Rearranging gives:
CvRV0f′(V0)+(1+CvR)P0>0
This implies that:
f′(V0)>−γP0V0
Thus, if f′(V0) (the slope of the curve) is greater than −γP0V0 (the slope of the adiabatic process), the gas is absorbing heat at the point (P0,V0).
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMODYNAMICS EXERCISE - SHORT ANSWER TYPE QUESTIONS6videos
THERMODYNAMICS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions15videos
THERMAL PROPERTIES OF MATTER
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - UNITS AND MEASUREMENTS EXERCISE - Long Answer Type Questions9videos
UNITS AND MEASUREMENTS
Similar Questions
A curve y=f(x) passes through point P(1,1) . The normal to the curve at P is a (y−1)+(x−1)=0 . If the slope of the tangent at any point on the curve is proportional to the ordinate of the point, then the equation of the curve is
View SolutionFor a p-V plot, the slope of an adiabatic curve = x × slope of isothermal at the same point. Here x is :
View SolutionThe slope of P-V graph for isochoric process is
View SolutionIf normal at P on the curve y2−3x2+y+10=0 passes through the point (0,32) ,then slope of tangent at P is n. The value of |n| is equal to
View SolutionIn process T∝1V, pressure of the gas increases from p0 to 4p0. Match the following.
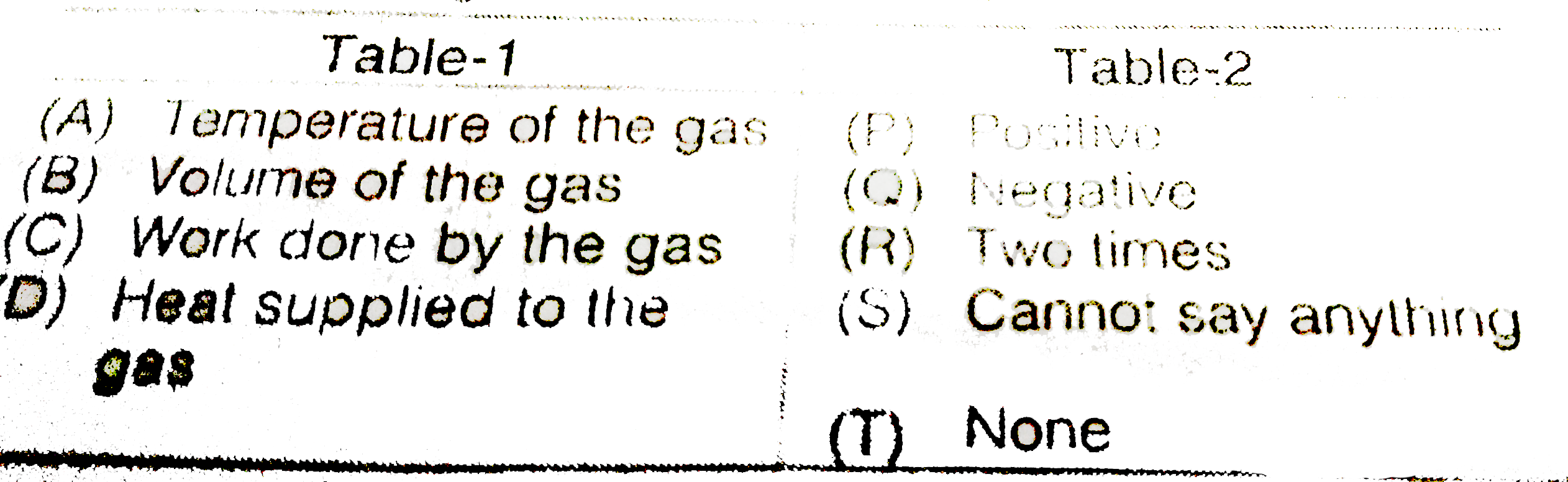 View Solution
View SolutionAn ideal monatomic gas is at P0,V0. It is taken to final volume 2V0 when pressure is P0/2 in a process which is straight line on P−V diagram. Then
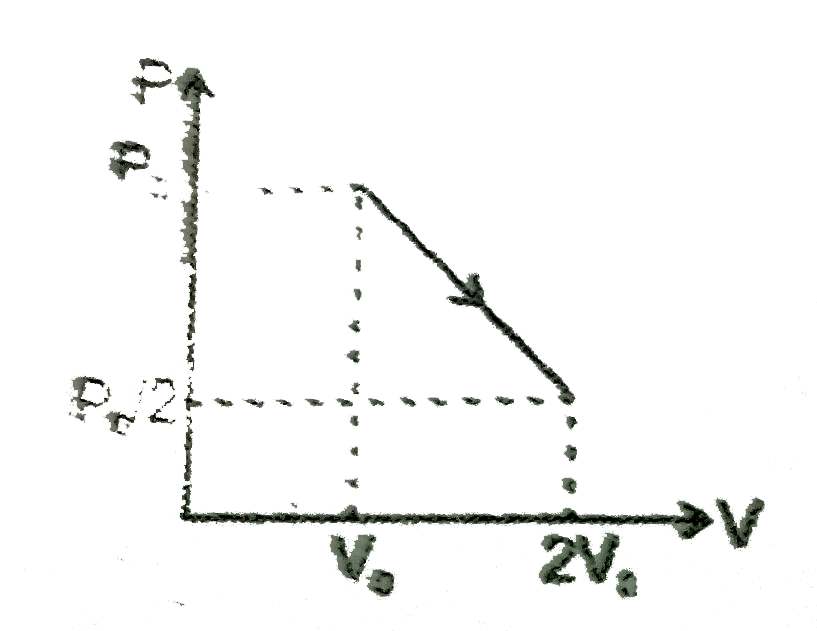 View Solution
View SolutionThe internal energy of a gas is given by U = 3 pV. It expands from V0 to 2V0 against a constant pressure p0.
The heat absorbed by the gas in the process isView SolutionThe internal energy of a gas is given by U = 3 pV. It expands from V0 to 2V0 against a constant pressure p0.
What is the value of γ(=CP/CV) for the given gas?View SolutionConider a given sample of an ideal gas (CpCv=γ) having initial pressure (p0)andvolume(V0) . (a) The gas is isothermally taken to a pressure (P02) and from there adiabatically ta a pressure (p02) and from there isothermally to a pressure (p04) . find the volume.
View SolutionOne mole of an ideal gas has an interal energy given by U=U0+2PV , where P is the pressure and V the volume of the gas. U0 is a constant. This gas undergoes the quasi− static cyclic process ABCD as shown in the U−V diagram. The work done by the ideal gas in the process AB is

View Solution

