Question

A semi-circular sheet of metal of diameter 28cm is
bent into an open conical cup. Find the depth and capacity of cup.

Explanation

Given,diameter of a semi-circular sheet = 28 cm
`therefore` Radius of a semi-circular sheet , `r =(28)/(2) = 14 cm`
Since, a semi -circular sheet of metal is bent to from an open conical cup.
let the d radius of a conical cup be R.

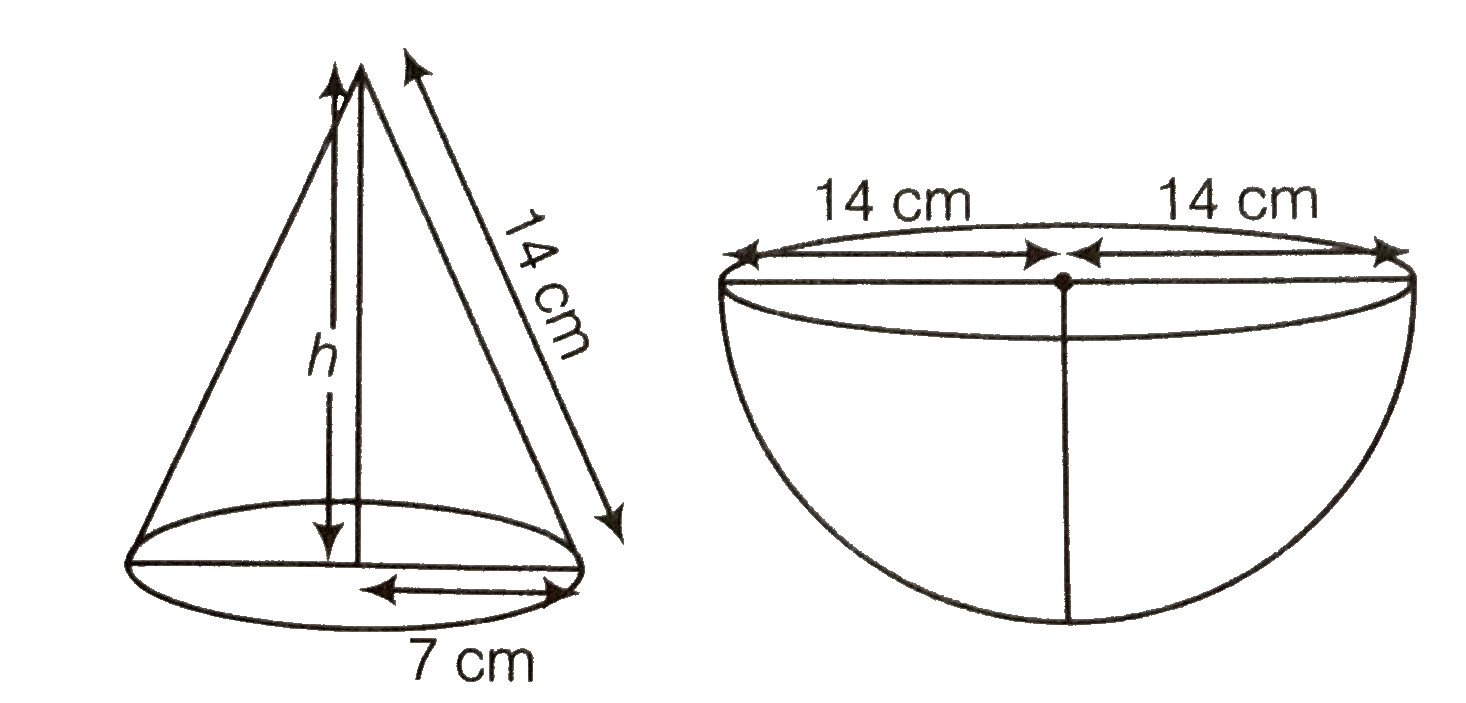
` therefore` Circumference of bases of cone = Circumference of semi- circle
` 2 piR = pi r`
`rArr" "2piR = pi xx 14 rArr R = 7 cm`
Now, `h =sqrt(l^(2) - R^(2)) = sqrt(14^(2) - 7^(2))" " [because l^(2) = h^(2) + R^(3)]`
`= sqrt(= 196-49) = sqrt(147) = 12.1243cm`
Volume (capacity ) of conical cup `= (1)/(3) piR^(2)h`
`= (1)/(3) xx (22)/(7) xx7 xx7 xx12.1243 = 622.38 cm^(3)`.
Hence, the capacity of an open conical cup is `622.38 cm^(3)`.