In the formula ¯x=a+∑fidi∑fi
for finding the mean of grouped data di'S and deviation from a of
lower limits of the classes
upper limits of the classes
mid-points of the classes
frequencies of the class marks
The correct Answer is:C
To solve the question regarding the formula for finding the mean of grouped data, we need to understand the components of the formula:
The formula given is:
¯x=a+∑fidi∑fi
where:
- ¯x is the mean of the grouped data,
- a is a constant (usually the assumed mean or the midpoint of the class),
- fi is the frequency of each class,
- di is the deviation of the class midpoint from a.
1. Identify the Components:
- Recognize that di represents the deviation of the class midpoints from the assumed mean a.
- The deviations di can be calculated as di=xi−a, where xi is the midpoint of the class.
2. Calculate Class Midpoints:
- For each class interval, calculate the midpoint xi. The midpoint can be calculated using the formula:
xi=Lower limit+Upper limit2
3. Calculate Deviations:
- Once you have the midpoints, calculate the deviations di for each class:
di=xi−a
4. Multiply Deviations by Frequencies:
- For each class, multiply the deviation di by the corresponding frequency fi:
fidi
5. Sum the Products:
- Sum all the products fidi to get ∑fidi.
6. Sum the Frequencies:
- Sum all the frequencies to get ∑fi.
7. Substitute into the Formula:
- Substitute the values of a, ∑fidi, and ∑fi into the formula:
¯x=a+∑fidi∑fi
8. Calculate the Mean:
- Perform the calculations to find ¯x, the mean of the grouped data.
¯x=a+∑fidi∑fi
where:
- ¯x is the mean of the grouped data,
- a is a constant (usually the assumed mean or the midpoint of the class),
- fi is the frequency of each class,
- di is the deviation of the class midpoint from a.
- Recognize that di represents the deviation of the class midpoints from the assumed mean a.
- The deviations di can be calculated as di=xi−a, where xi is the midpoint of the class.
- For each class interval, calculate the midpoint xi. The midpoint can be calculated using the formula:
xi=Lower limit+Upper limit2
- Once you have the midpoints, calculate the deviations di for each class:
di=xi−a
- For each class, multiply the deviation di by the corresponding frequency fi:
fidi
- Sum all the products fidi to get ∑fidi.
- Sum all the frequencies to get ∑fi.
- Substitute the values of a, ∑fidi, and ∑fi into the formula:
¯x=a+∑fidi∑fi
- Perform the calculations to find ¯x, the mean of the grouped data.
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - VERY SHORT ANSWERS QUESTIONS
14 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - SHORT ANSWERS QUESTIONS
42 Videos
- REAL NUMBERSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
In the formula ¯x=a+(∑fiui∑fi)×h,ui=
View SolutionIn the formula ¯x=a+h∑fiui∑fi
for finding the mean of grouped frequency distribution ui is equal to
View SolutionIn Calculating the mean of grouped data, grouped in classes of equal width, we may use the formula
¯x=a+∑fidi∑fi
Where, a is the assumed mean, a must be one of the mid point of the classes. Is the last statement correct? Justify your answer.
View SolutionFind the mean and standard deviation from the following data :

View SolutionIf for distribution of 18 observations ∑(xi−5)=3and∑(xi−5)2=43, find the mean and standard deviation.
View SolutionIf for distribution of 18 observations ∑(xi−5)=3and∑(xi−5)2=43, find the mean and standard deviation.
View SolutionFind the mean deviation from the mean for the following data:

View SolutionLet 1x1,x2….xn be n obervations .Let wi=lxi+k for i=1,2….n,where l and k are constants. If the mean of xi is 48 and their standard deviation is 12 the mean of wi 's is 55 and standard deviation of wi is 15 then the value of l and k should be
View SolutionFind the mean deviation from the median for the following data:
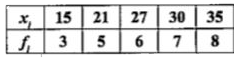
View SolutionFind the mean deviation from the mean for the followinng data:

View Solution
