Suppose 10000 tickets are sold in a lottery each for ₹ 1. First prize is of ₹ 3000 and the second prize is of ₹ 2000. There are three third prizes of ₹ 500 each. If you buy one ticket, then what is your expectation?
To find the expectation of winning when buying one ticket in the lottery, we can follow these steps:
Step 1: Identify the Prizes and Their Values
- First Prize: ₹3000 (1 winner)
- Second Prize: ₹2000 (1 winner)
- Third Prize: ₹500 (3 winners)
Step 2: Determine the Total Number of Tickets
The total number of tickets sold is 10,000.
Step 3: Calculate the Probability of Winning Each Prize
- Probability of winning the first prize (₹3000):
P(3000)=110000
- Probability of winning the second prize (₹2000):
P(2000)=110000
- Probability of winning a third prize (₹500):
P(500)=310000
Step 4: Create a Probability Distribution Table
| Prize (₹) | Probability (P) |
|-----------|-------------------------|
| 3000 | 110000 |
| 2000 | 110000 |
| 500 | 310000 |
Step 5: Calculate the Expected Value (E)
The expected value is calculated using the formula:
E(X)=∑(x⋅P(x))
Calculating each term:
- For the first prize:
3000⋅110000=300010000=0.3
- For the second prize:
2000⋅110000=200010000=0.2
- For the third prize:
500⋅310000=150010000=0.15
Step 6: Sum the Expected Values
Now, we sum these expected values:
E(X)=0.3+0.2+0.15=0.65
Conclusion
The expected value of winning when buying one ticket is ₹0.65.
---
- First Prize: ₹3000 (1 winner)
- Second Prize: ₹2000 (1 winner)
- Third Prize: ₹500 (3 winners)
The total number of tickets sold is 10,000.
- Probability of winning the first prize (₹3000):
P(3000)=110000
- Probability of winning the second prize (₹2000):
P(2000)=110000
- Probability of winning a third prize (₹500):
P(500)=310000
| Prize (₹) | Probability (P) |
|-----------|-------------------------|
| 3000 | 110000 |
| 2000 | 110000 |
| 500 | 310000 |
The expected value is calculated using the formula:
E(X)=∑(x⋅P(x))
- For the first prize:
3000⋅110000=300010000=0.3
2000⋅110000=200010000=0.2
500⋅310000=150010000=0.15
Now, we sum these expected values:
E(X)=0.3+0.2+0.15=0.65
The expected value of winning when buying one ticket is ₹0.65.
Topper's Solved these Questions
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Long Answer Type Questions
15 Videos
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Objective Type Questions
38 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
- RELATIONS AND FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Fillers
15 Videos
Similar Questions
In a lottery 10,000 tickets are sold and ten equal prizes are awarded,. What is the probability of not getting a prove if you buy i. 1 ticket ii. two tickets iii. 10 tickets.
View SolutionIn a lottery 10,000 tickets are sold and ten equal prizes are awarded,. What is the probability of not getting a prove if you buy i. 1 ticket ii. two tickets iii. 10 tickets.
View Solution1000 tickets of a lottery were sold and there are 5 prizes on these tickets. If Saket has purchased one lottery ticket, what is the probability of winning a prize?
View SolutionThere are 15 prizes and 25 blaks in a lottery. Find the probability of getting a prize on one ticket.
View SolutionThree prizes are to be distributed in a quiz contest. The value of the second prize is five sixths the value of the first prize and the value of the third prize is four-fifths that of the second prize. If the total value of three prizes is Rs 150, find the value of each prize.
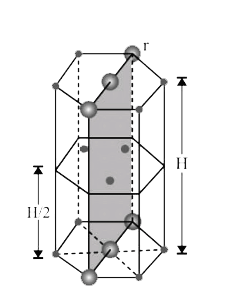
View SolutionIn a hexagonal system system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-packed is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed overt the first layer so that they touch each other and represent the second layer so that they touch each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is converted with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
(a)4
(b)6
(c)12
(d)17
View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The volume of this HCP unit cell is

View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The empty space in this HCP unit cell is :
View SolutionAn aeroplane can carry a maximum of 200 passengers. A profit of Rs. 400 is made on each first class ticket and a profit of Rs. 300 is made on each second class ticket. The airline reserves at least 20 seats for first class. However, at least four times as many passengers prefer to travel by second class then by first class. Determine how many tickets of each type must be sold to maximise profit for the airline. Form an LPP and solve it graphically.
View SolutionTwo institutions decided to award their employees for the three values of resourcefulness, competence and determination in the form of prizes at the rate of Rs x, y and z respectively per person. The first institution decided to award respectively 4, 3 and 2 employees with a total prize money of Rs 37000 and the second institution decided to award respectively 5, 3 and 4 employees with a total prize money of Rs 47000. If all the three prizes per person together amount to Rs 12000, then using matrix method find the value of x, y, and z. What values are described in this equations?
View Solution
