Find the area of region by the curve y=sinx between x=0 and x=2π.
The correct Answer is:N/a
Required area =∫2π0sinxdx=∫π0sinxsx+∣∣∣∫2ππsinxdx∣∣∣
−[cosc]π0+∣∣[−cosx]2ππ∣∣
=−[cosπ−cos0]+|−[cos2π−cosπ]|
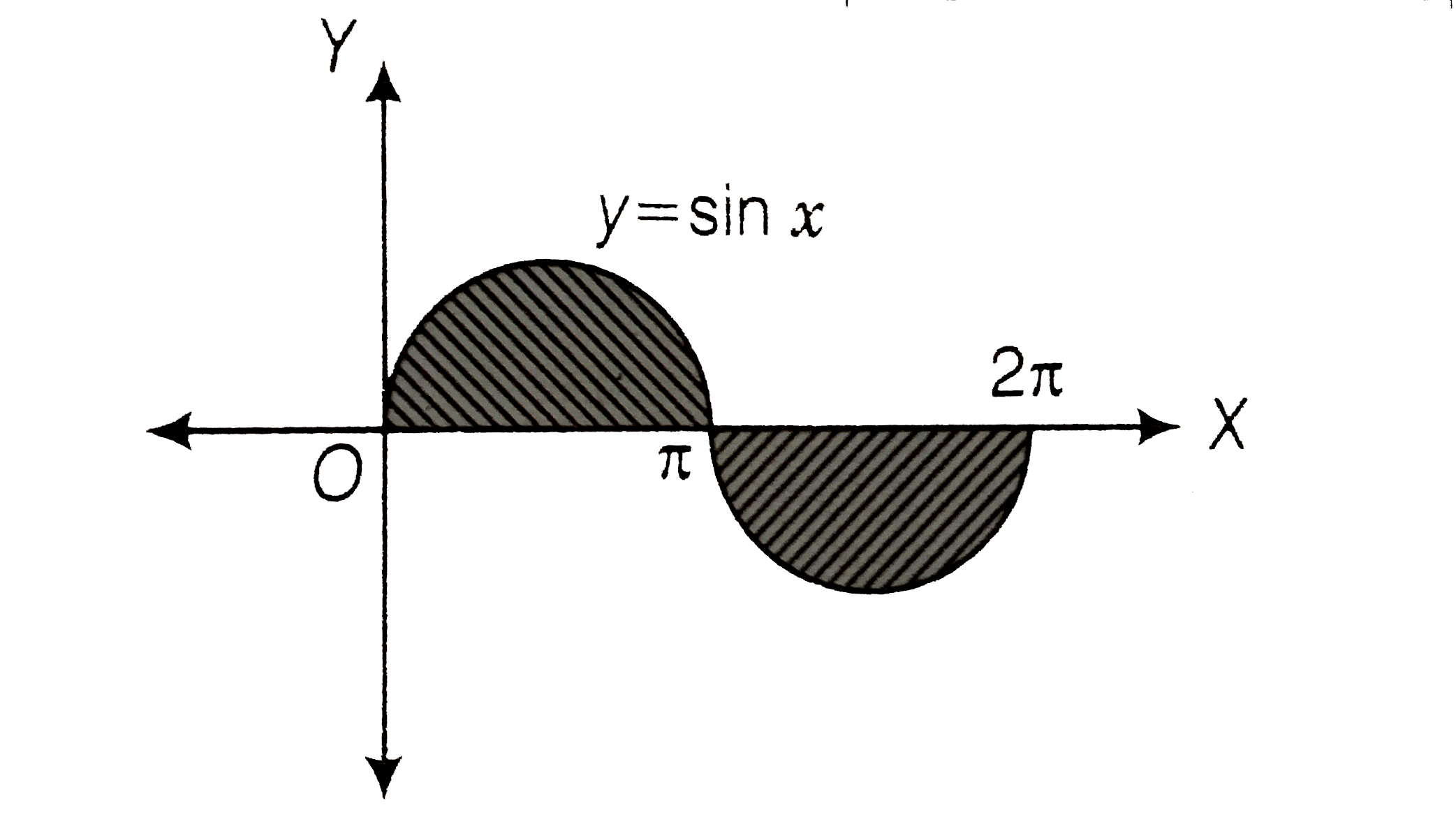
=−[−1−1]+ABS(−(1+1))
=2+2=4 sq units
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Objective Type Questions22videos
APPLICATION OF INTEGRALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Objective Type Questions22videos
APPLICATION OF INTEGRALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Fillers5videos
APPLICATION OF DERIVATIVES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - True/False10videos
CONTINUITY AND DIFFERENTIABILITY
Similar Questions
Find the area bounded by the curve y=cosxbetween x=0and x=2π.
View SolutionFind the area of the region bounded by the curve y=sinx between x=0andx=2π.
View SolutionFind the area enclosed the curve y=sin x and the X-axis between x=0andx=π.
View SolutionFind the area enclosed the curve y=sin x and the X-axis between x=0andx=π.
View SolutionFind the area of the region bounded by the curve y=x3,y=x+6 and x=0
View SolutionFind the area between the curve y=x and y=x2
View SolutionFind the area of region bounded by the curve ay2=x3, the y-axis and the lines y=aandy=2a.
View SolutionArea of the regionbounded by the curve y=cosx between x=0 and x=π is
View SolutionThe area of the region bounded by the curve y=sinx between the ordinates x=0, x=π2 and the X−axis is
View SolutionFind the area of the region bounded by the curve y=sinx,x=π2andx=3π2
View Solution

