Show that the height of a closed right circular cylinder of given surface and maximum volume, is equal to the diameter of its base.
To show that the height h of a closed right circular cylinder of given surface area A and maximum volume V is equal to the diameter of its base, we can follow these steps:
Step 1: Define the Variables
Let:
- r = radius of the base of the cylinder
- h = height of the cylinder
- A = total surface area of the cylinder
- V = volume of the cylinder
Step 2: Write the Formulas
The surface area A of a closed cylinder is given by:
A=2πrh+2πr2
The volume V of the cylinder is given by:
V=πr2h
Step 3: Express Height in Terms of Radius
From the surface area formula, we can express h in terms of r and A:
h=A−2πr22πr
Step 4: Substitute h into the Volume Formula
Now, substitute h into the volume formula:
V=πr2(A−2πr22πr)
This simplifies to:
V=r(A−2πr2)2
V=Ar2−πr3
Step 5: Differentiate the Volume with Respect to r
To find the maximum volume, we differentiate V with respect to r:
dVdr=A2−3πr2
Step 6: Set the Derivative Equal to Zero
Set the derivative equal to zero to find the critical points:
A2−3πr2=0
Solving for r:
3πr2=A2
r2=A6π
r=√A6π
Step 7: Substitute r Back to Find h
Now substitute r back into the equation for h:
h=A−2π(A6π)2π√A6π
This simplifies to:
h=A−A32π√A6π
h=2A32π√A6π
h=A3π√A6π
Step 8: Relate h to r
Now, we need to show that h=2r:
Substituting r into h:
h=2√A6π
Since 2r=2√A6π, we have:
h=2r
Step 9: Verify Maximum Volume Condition
To confirm that this is indeed a maximum, we check the second derivative:
d2Vdr2=−6πr
Since r>0, d2Vdr2<0, confirming that we have a maximum.
Conclusion
Thus, we have shown that the height h of a closed right circular cylinder of given surface area and maximum volume is equal to the diameter of its base:
h=2r
Let:
- r = radius of the base of the cylinder
- h = height of the cylinder
- A = total surface area of the cylinder
- V = volume of the cylinder
The surface area A of a closed cylinder is given by:
A=2πrh+2πr2
The volume V of the cylinder is given by:
V=πr2h
From the surface area formula, we can express h in terms of r and A:
h=A−2πr22πr
Now, substitute h into the volume formula:
V=πr2(A−2πr22πr)
This simplifies to:
V=r(A−2πr2)2
V=Ar2−πr3
To find the maximum volume, we differentiate V with respect to r:
dVdr=A2−3πr2
Set the derivative equal to zero to find the critical points:
A2−3πr2=0
Solving for r:
3πr2=A2
r2=A6π
r=√A6π
Now substitute r back into the equation for h:
h=A−2π(A6π)2π√A6π
This simplifies to:
h=A−A32π√A6π
h=2A32π√A6π
h=A3π√A6π
Now, we need to show that h=2r:
Substituting r into h:
h=2√A6π
Since 2r=2√A6π, we have:
h=2r
To confirm that this is indeed a maximum, we check the second derivative:
d2Vdr2=−6πr
Since r>0, d2Vdr2<0, confirming that we have a maximum.
Thus, we have shown that the height h of a closed right circular cylinder of given surface area and maximum volume is equal to the diameter of its base:
h=2r
Topper's Solved these Questions
Similar Questions
Show that the radius of closed right circular cylinder of given surface area maximum volume is equal to half of its height.
View SolutionShow that the right circular cylinder, open at the top, and of given surface area and maximum volume is such that its height is equal to the radius of the base.
View Solution
Knowledge Check
The height and radius of the right circular cylinder below are given in meters. What is the volume, in cubic meters, of the cylinder?
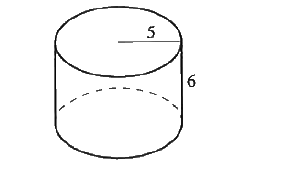 A30πB31πC150πD180π
A30πB31πC150πD180π
Show that the right circular cylinder, open at the top, and of given surface area and maximum volume is such that its height is equal to the radius of the base.
View SolutionShow that right circular cone of least curved surface and given volume has an altitude equal to √2 times the radius of the base.
View SolutionShow that the right-circular cone of least curved surface and given volume has an altitude equal to √2 times the radius of the base.
View SolutionShow that the height of the right circular cylinder of maximum volume that can be inscribed in a given right circular cone of height h is h3
View SolutionShow that semi-vertical angle of right circular cone of given total surface area and maximum volume is sin−113.
View SolutionShow that the height of the right circular cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm.
View SolutionA sphere and a right circular cylinder of the same radius have equal volume. By what percentage does the diameter of the cylinder exceed its height ?
View Solution