The random variable X can the values 0, 1, 2, 3, Give P(X = 0) = P(X = 1)= p and P(X = 2) = P(X = 3) such that ∑pix2i=2∑pixi then find the value of p
To solve the problem, we need to find the value of p given the conditions on the random variable X and its probabilities. Let's break down the solution step by step.
Step 1: Define the probabilities
Let:
- P(X=0)=p
- P(X=1)=p
- P(X=2)=k
- P(X=3)=k
Step 2: Set up the equation for total probability
Since the total probability must equal 1, we have:
P(X=0)+P(X=1)+P(X=2)+P(X=3)=1
This gives us:
p+p+k+k=1⟹2p+2k=1⟹p+k=12(1)
Step 3: Set up the equation for the second condition
We are given that:
∑pix2i=2∑pixi
Calculating ∑pix2i:
∑pix2i=P(X=0)⋅02+P(X=1)⋅12+P(X=2)⋅22+P(X=3)⋅32
Substituting the probabilities:
=p⋅0+p⋅1+k⋅4+k⋅9=p+4k+9k=p+13k(2)
Calculating ∑pixi:
∑pixi=P(X=0)⋅0+P(X=1)⋅1+P(X=2)⋅2+P(X=3)⋅3
Substituting the probabilities:
=p⋅0+p⋅1+k⋅2+k⋅3=p+2k+3k=p+5k(3)
Step 4: Set up the equation from the condition
From the condition ∑pix2i=2∑pixi, we have:
p+13k=2(p+5k)
Expanding and simplifying:
p+13k=2p+10k⟹13k−10k=2p−p⟹3k=p(4)
Step 5: Substitute equation (4) into equation (1)
Substituting p=3k into p+k=12:
3k+k=12⟹4k=12⟹k=18
Step 6: Find p
Using k=18 in equation (4):
p=3k=3⋅18=38
Final Answer
Thus, the value of p is:
38
Let:
- P(X=0)=p
- P(X=1)=p
- P(X=2)=k
- P(X=3)=k
Since the total probability must equal 1, we have:
P(X=0)+P(X=1)+P(X=2)+P(X=3)=1
This gives us:
p+p+k+k=1⟹2p+2k=1⟹p+k=12(1)
We are given that:
∑pix2i=2∑pixi
Calculating ∑pix2i:
∑pix2i=P(X=0)⋅02+P(X=1)⋅12+P(X=2)⋅22+P(X=3)⋅32
Substituting the probabilities:
=p⋅0+p⋅1+k⋅4+k⋅9=p+4k+9k=p+13k(2)
∑pixi=P(X=0)⋅0+P(X=1)⋅1+P(X=2)⋅2+P(X=3)⋅3
Substituting the probabilities:
=p⋅0+p⋅1+k⋅2+k⋅3=p+2k+3k=p+5k(3)
From the condition ∑pix2i=2∑pixi, we have:
p+13k=2(p+5k)
Expanding and simplifying:
p+13k=2p+10k⟹13k−10k=2p−p⟹3k=p(4)
Substituting p=3k into p+k=12:
3k+k=12⟹4k=12⟹k=18
Using k=18 in equation (4):
p=3k=3⋅18=38
Thus, the value of p is:
38
Topper's Solved these Questions
Similar Questions
Knowledge Check
A random variable X takes the values 0,1,2,3 and its mean = 1,3 .If P(X=3) =2P(X=1) and P(X=2) = 0.3 then P(X=0) is
A0.4B0.3C0.2D0.1
The random variable X can take only the values 0,1,2. If
P(X=0)=P(X=1)=pandE(X2)=E[X],
then find valu of p.
View SolutionA random variate X takes the values 0, 1, 2, 3 and its mean is 1.3. If P(X=3)=2P(X=1) and P(X=2)=0.3, then P(X=0) is equal to
View SolutionA random variable X takes values 0, 1, 2, 3,… with probability proportional to (x+1)(15)x.
P(X≥2) equals
View SolutionThe probability of a random variable X is given below
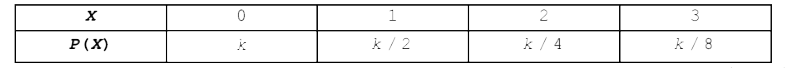
Find P(X≤2)+P(X>2)
View SolutionThe range of a random variable X is {0, 1, 2}. Given that P(X=0)=3c3,P(X=1)=4c−10c2,P(X=2)=5c−1 where c is constant.
Find (i) the value of c (ii) P(X<1)
(iii) P(1<X≤2) (iv) P(0<X≤3)
View SolutionA binomial random variable X, 5P(X = 3) = 2P(X = 2), when n = 5. Find the value of parameter p.
View SolutionIf X is a Poisson variate with
P(X=2)=23P(X=1), find P(X=0) and P(X=3)
View Solution
