A company produces two types of goods A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of type B requires 1 g of silver and 2 g of gold. The company can procure a maximum of 9 g of silver and 8 g of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, formulate LPP to maximize profit.
To formulate the Linear Programming Problem (LPP) for maximizing profit from the production of goods A and B, we will follow these steps:
Step 1: Define the Variables
Let:
- x = number of units of product A produced
- y = number of units of product B produced
Step 2: Define the Objective Function
The profit from each unit of product A is Rs 40, and from product B is Rs 50. Therefore, the total profit Z can be expressed as:
Z=40x+50y
We aim to maximize Z.
Step 3: Define the Constraints
From the problem statement, we know the following constraints based on the resources available:
1. Silver Constraint: Each unit of A requires 3 g of silver and each unit of B requires 1 g of silver. The total available silver is 9 g. Therefore, the constraint can be written as:
3x+y≤9
2. Gold Constraint: Each unit of A requires 1 g of gold and each unit of B requires 2 g of gold. The total available gold is 8 g. Therefore, the constraint can be written as:
x+2y≤8
3. Non-negativity Constraints: Since the production of goods cannot be negative, we have:
x≥0
y≥0
Step 4: Formulate the LPP
Combining the objective function and the constraints, we can summarize the LPP as follows:
Maximize:
Z=40x+50y
Subject to:
3x+y≤9
x+2y≤8
x≥0
y≥0
Step 5: Solve the LPP
To find the feasible region, we can graph the constraints and identify the corner points.
1. Graph the constraints:
- For 3x+y=9:
- If x=0, then y=9 (point (0, 9))
- If y=0, then x=3 (point (3, 0))
- For x+2y=8:
- If x=0, then y=4 (point (0, 4))
- If y=0, then x=8 (point (8, 0))
2. Find intersection of the constraints:
To find the intersection of the lines 3x+y=9 and x+2y=8:
- From 3x+y=9, we can express y as y=9−3x.
- Substitute into x+2y=8:
x+2(9−3x)=8
x+18−6x=8
−5x=−10⟹x=2
- Substitute x=2 back into y=9−3(2):
y=3
Thus, the intersection point is (2, 3).
3. Evaluate the objective function at the corner points:
- For (0, 0): Z=40(0)+50(0)=0
- For (0, 4): Z=40(0)+50(4)=200
- For (2, 3): Z=40(2)+50(3)=80+150=230
- For (3, 0): Z=40(3)+50(0)=120
Step 6: Determine Maximum Profit
The maximum profit occurs at the point (2, 3) with a profit of Rs 230.
Final Answer
The LPP is formulated as follows:
- Maximize: Z=40x+50y
- Subject to:
- 3x+y≤9
- x+2y≤8
- x≥0
- y≥0
The maximum profit is Rs 230 when producing 2 units of product A and 3 units of product B.
Let:
- x = number of units of product A produced
- y = number of units of product B produced
The profit from each unit of product A is Rs 40, and from product B is Rs 50. Therefore, the total profit Z can be expressed as:
Z=40x+50y
We aim to maximize Z.
From the problem statement, we know the following constraints based on the resources available:
3x+y≤9
x+2y≤8
x≥0
y≥0
Combining the objective function and the constraints, we can summarize the LPP as follows:
Z=40x+50y
3x+y≤9
x+2y≤8
x≥0
y≥0
To find the feasible region, we can graph the constraints and identify the corner points.
- For 3x+y=9:
- If x=0, then y=9 (point (0, 9))
- If y=0, then x=3 (point (3, 0))
- If x=0, then y=4 (point (0, 4))
- If y=0, then x=8 (point (8, 0))
To find the intersection of the lines 3x+y=9 and x+2y=8:
- From 3x+y=9, we can express y as y=9−3x.
- Substitute into x+2y=8:
x+2(9−3x)=8
x+18−6x=8
−5x=−10⟹x=2
- Substitute x=2 back into y=9−3(2):
y=3
Thus, the intersection point is (2, 3).
- For (0, 0): Z=40(0)+50(0)=0
- For (0, 4): Z=40(0)+50(4)=200
- For (2, 3): Z=40(2)+50(3)=80+150=230
- For (3, 0): Z=40(3)+50(0)=120
The maximum profit occurs at the point (2, 3) with a profit of Rs 230.
The LPP is formulated as follows:
- Maximize: Z=40x+50y
- Subject to:
- 3x+y≤9
- x+2y≤8
- x≥0
- y≥0
Topper's Solved these Questions
Similar Questions
A company produces two types of good, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs. 40 and that of type B Rs. 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
View SolutionA company produces two types of items, and Q. Manufacturing of both items requires the metals gold and copper. Each unit of item P requires 3 gm of gold and 1 gm of copper while that of item Q requires 1 gm of gold and 2 gm of copper. The company has 9 gm of gold and 8 gm of copper in its store. If each unit of item P makes a profit of Rs 50 and each unit of item O makes a profit of 60, determine the number of units of each item that the company should produce to maximize profit. What is the maximum profit?
View SolutionA company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is Rs. 40 on each unit of product of type A and Rs. 50 on each unit of type B. How many units of each type should the company manufacture so as to earn maximum profit ? Use linear programming to find the solution.
View SolutionA company manufactures two types of toys A and B. A toy of type A requires 5 minute for cutting and 10 minute for assembling. A toy of type B requires 8 minute for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling th etoys in a day. The profit is Rs 50 each on a toy of Type A and Rs 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit ? Use linear programming to find the solution.
View SolutionWhat is the hydrometallurgy of silver or gold commonly known as ?
View SolutionWhat is the hydrometallurgy of silver or gold commonly known as ?
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
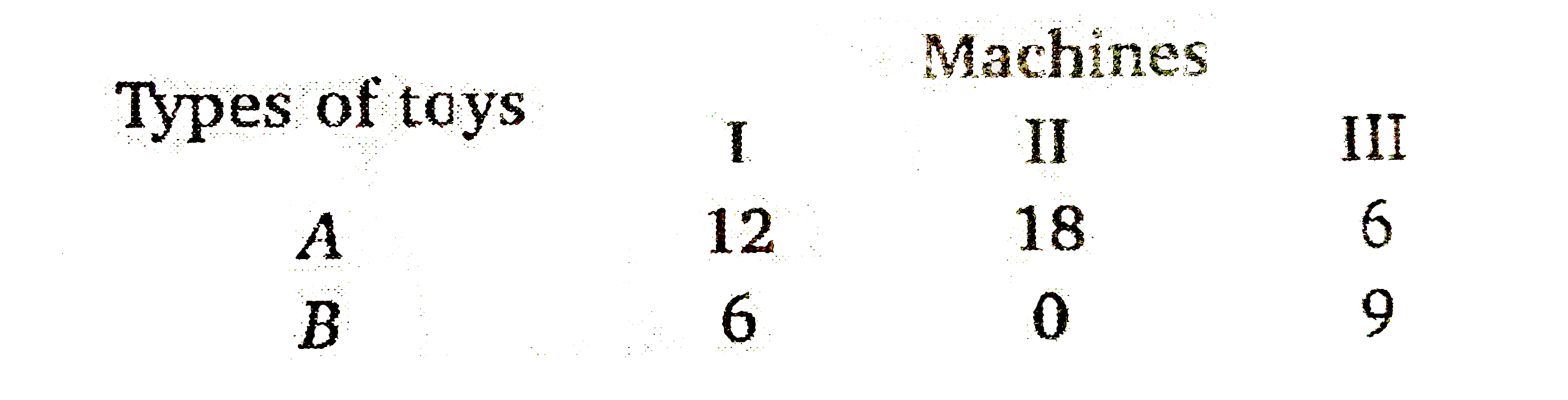
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionDensity of silver is 10.5 g ^(−1) Calculate the edge length of the unit cell of silver.
View SolutionThe ratio between weights of gold and silver in an alloy is 17:3. If the weight of silver in the alloy is 2.7g, find :
the ratio of weight of gold to that of alloy.
View SolutionThe ratio between weights of gold and silver in an alloy is 17:3. If the weight of silver in the alloy is 2.7g, find :
the weight of gold in the alloy.
View Solution
