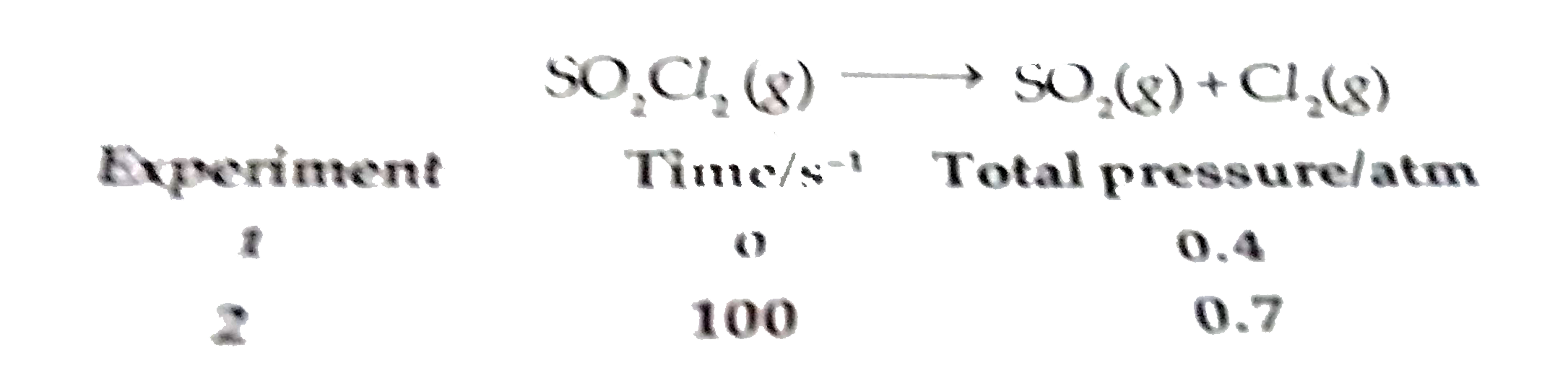The following data were obtained during the first order thermal decomposition of SO2Cl2 at constant volume :
ExperimentTime (s)Total Pressure (atm)100.321000.5
Calculate rate constant
[Given : log 6 = 0.7782, log 3 = 0.4771]
To calculate the rate constant for the first-order thermal decomposition of SO2Cl2, we will follow these steps:
Step 1: Write the decomposition reaction
The thermal decomposition of SO2Cl2 can be represented as:
SO2Cl2(g)→SO2(g)+Cl2(g)
Step 2: Define initial and final conditions
- At time t=0:
- Total pressure P0=0.3atm
- SO2Cl2 pressure = P0
- SO2 pressure = 0
- Cl2 pressure = 0
- At time t=100s:
- Total pressure Pt=0.5atm
- Let p be the pressure of SO2 and Cl2 formed.
Step 3: Relate pressures
From the reaction stoichiometry:
- The change in pressure due to the decomposition of SO2Cl2 can be expressed as:
Pt=P0−(P0−Pt)+p+p
This simplifies to:
Pt=P0+p
Thus, we can express p as:
p=Pt−P0
Step 4: Calculate p
Substituting the values:
p=0.5atm−0.3atm=0.2atm
Step 5: Calculate P0−p
Now, we can calculate P0−p:
P0−p=0.3atm−0.2atm=0.1atm
Step 6: Use the first-order rate constant formula
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(P0P0−p)
Substituting the values:
- t=100s
- P0=0.3atm
- P0−p=0.1atm
Step 7: Calculate k
k=2.303100log(0.30.1)
Calculating the logarithm:
log(0.30.1)=log(3)≈0.4771
Now substituting this back into the equation:
k=2.303100×0.4771≈0.01099s−1
Calculating further:
k≈1.099×10−2s−1
Final Result
Thus, the rate constant k for the decomposition of SO2Cl2 is approximately:
k≈1.10×10−2s−1
The thermal decomposition of SO2Cl2 can be represented as:
SO2Cl2(g)→SO2(g)+Cl2(g)
- At time t=0:
- Total pressure P0=0.3atm
- SO2Cl2 pressure = P0
- SO2 pressure = 0
- Cl2 pressure = 0
- Total pressure Pt=0.5atm
- Let p be the pressure of SO2 and Cl2 formed.
From the reaction stoichiometry:
- The change in pressure due to the decomposition of SO2Cl2 can be expressed as:
Pt=P0−(P0−Pt)+p+p
This simplifies to:
Pt=P0+p
Thus, we can express p as:
p=Pt−P0
Substituting the values:
p=0.5atm−0.3atm=0.2atm
Now, we can calculate P0−p:
P0−p=0.3atm−0.2atm=0.1atm
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(P0P0−p)
Substituting the values:
- t=100s
- P0=0.3atm
- P0−p=0.1atm
k=2.303100log(0.30.1)
Calculating the logarithm:
log(0.30.1)=log(3)≈0.4771
Now substituting this back into the equation:
k=2.303100×0.4771≈0.01099s−1
Calculating further:
k≈1.099×10−2s−1
Thus, the rate constant k for the decomposition of SO2Cl2 is approximately:
k≈1.10×10−2s−1
Similar Questions
Knowledge Check
- Question 1 - Select One
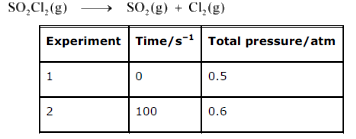
The following data were obtained during the first order thermal decomposition of SO2CI2 at a constant volume.
SO2CI2(g)→SO2(g)+CI2(g)
ExperimentTime/s−1Total pressure/atm100.521000.6
What is the rate of reaction when total pressure is 0.65 atm?A0.35atms−1B2.235×10−3atms−1C7.8×10−4atms−1D1.55×10−4atms−1
The following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
 View Solution
View SolutionThe following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣ ∣ ∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣ ∣ ∣∣
Calculate the rate constant.View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume :
SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate constant
( given : log 4=0.6021,log2=0.3010)View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume :
SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate constant
( given : log 4=0.6021,log2=0.3010)View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume :
SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate constant
( given : log 4=0.6021,log2=0.3010)View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
Calculate the rate of the reaction when total pressure is 0.65 atmView Solution