Write Einstein's photoelectric equation.
Write the three salient features observed in photoelectric effect which can be explained using this equation.
Step-by-Step Solution
1. Einstein's Photoelectric Equation:
The equation can be expressed as:
E=ϕ0+KEmax
where:
- E is the energy of the incident photon.
- ϕ0 is the work function of the metal (the minimum energy required to eject an electron).
- KEmax is the maximum kinetic energy of the emitted photoelectron.
The energy of the photon can also be expressed in terms of its frequency (ν):
E=hν
where h is Planck's constant.
Therefore, the complete equation can be rewritten as:
hν=ϕ0+KEmax
2. Deriving Maximum Kinetic Energy:
Rearranging the equation gives:
KEmax=hν−ϕ0
This shows that the maximum kinetic energy of the emitted electrons depends on the frequency of the incident light and the work function of the metal.
3. Threshold Frequency:
The threshold frequency (ν0) is defined as the minimum frequency required to eject an electron from the metal surface. It can be expressed as:
ϕ0=hν0
Thus, the equation can also be expressed as:
KEmax=h(ν−ν0)
4. Salient Features of Photoelectric Effect:
The three salient features that can be explained using Einstein's photoelectric equation are:
- Linear Relationship: The maximum kinetic energy of the emitted photoelectrons varies linearly with the frequency of the incident radiation. This means that as the frequency increases, the kinetic energy of the emitted electrons also increases.
- Threshold Frequency: No photoelectric effect is observed if the frequency of the incident light is below the threshold frequency (ν0). This means that there is a minimum frequency required to eject electrons from the metal surface.
- Instantaneous Emission: The photoelectric emission is an instantaneous process. When light of sufficient frequency strikes the metal surface, electrons are emitted immediately without any time delay.
The equation can be expressed as:
E=ϕ0+KEmax
where:
- E is the energy of the incident photon.
- ϕ0 is the work function of the metal (the minimum energy required to eject an electron).
- KEmax is the maximum kinetic energy of the emitted photoelectron.
E=hν
where h is Planck's constant.
hν=ϕ0+KEmax
Rearranging the equation gives:
KEmax=hν−ϕ0
This shows that the maximum kinetic energy of the emitted electrons depends on the frequency of the incident light and the work function of the metal.
The threshold frequency (ν0) is defined as the minimum frequency required to eject an electron from the metal surface. It can be expressed as:
ϕ0=hν0
Thus, the equation can also be expressed as:
KEmax=h(ν−ν0)
The three salient features that can be explained using Einstein's photoelectric equation are:
- Linear Relationship: The maximum kinetic energy of the emitted photoelectrons varies linearly with the frequency of the incident radiation. This means that as the frequency increases, the kinetic energy of the emitted electrons also increases.
- Threshold Frequency: No photoelectric effect is observed if the frequency of the incident light is below the threshold frequency (ν0). This means that there is a minimum frequency required to eject electrons from the metal surface.
- Instantaneous Emission: The photoelectric emission is an instantaneous process. When light of sufficient frequency strikes the metal surface, electrons are emitted immediately without any time delay.
Similar Questions
Knowledge Check
- Question 1 - Select One
According to Einstein's photoelectric equation , the graph between the kinetic energy of photoelectrons ejected and the frequency of incident radiation is
A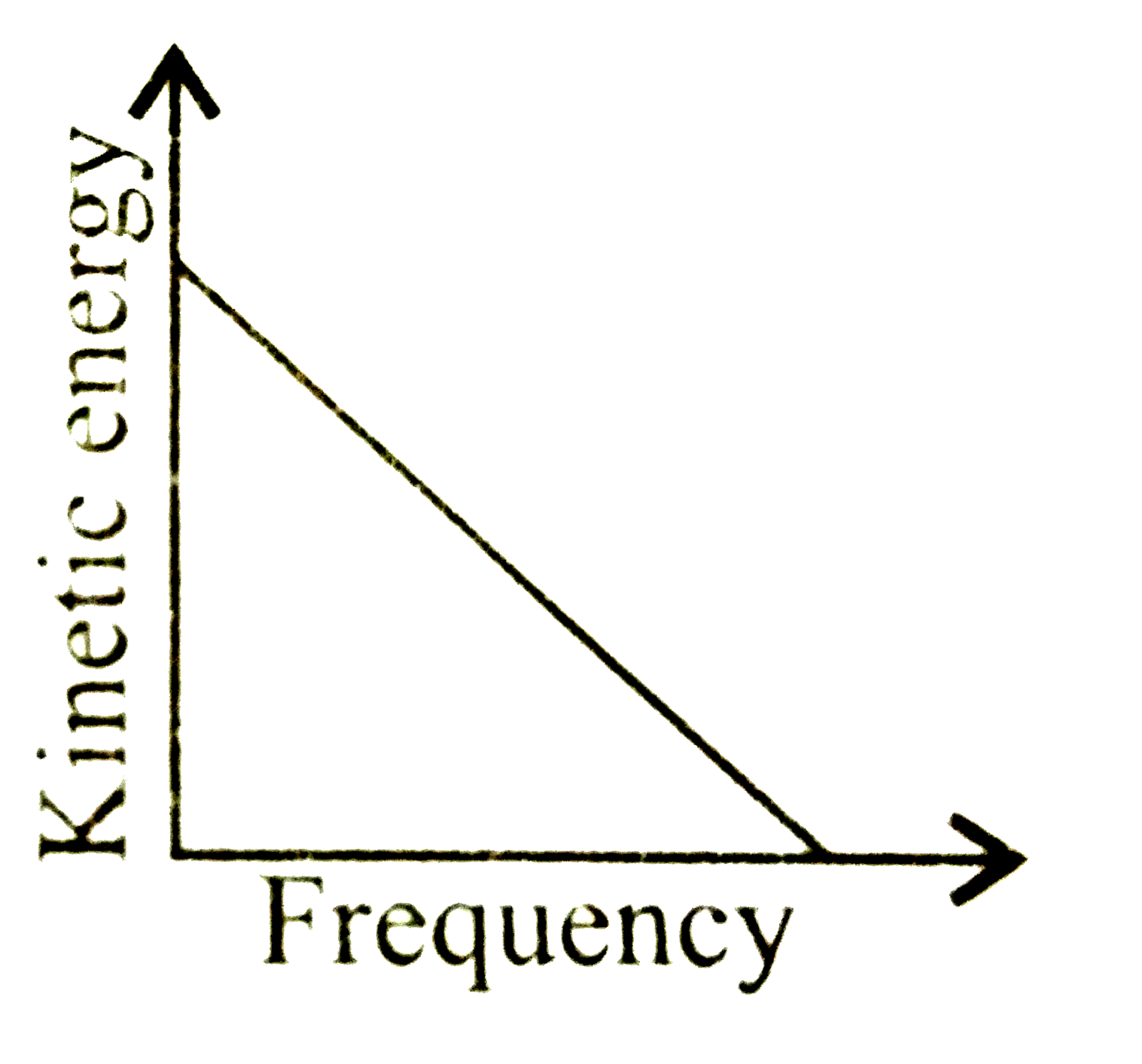 B
B C
C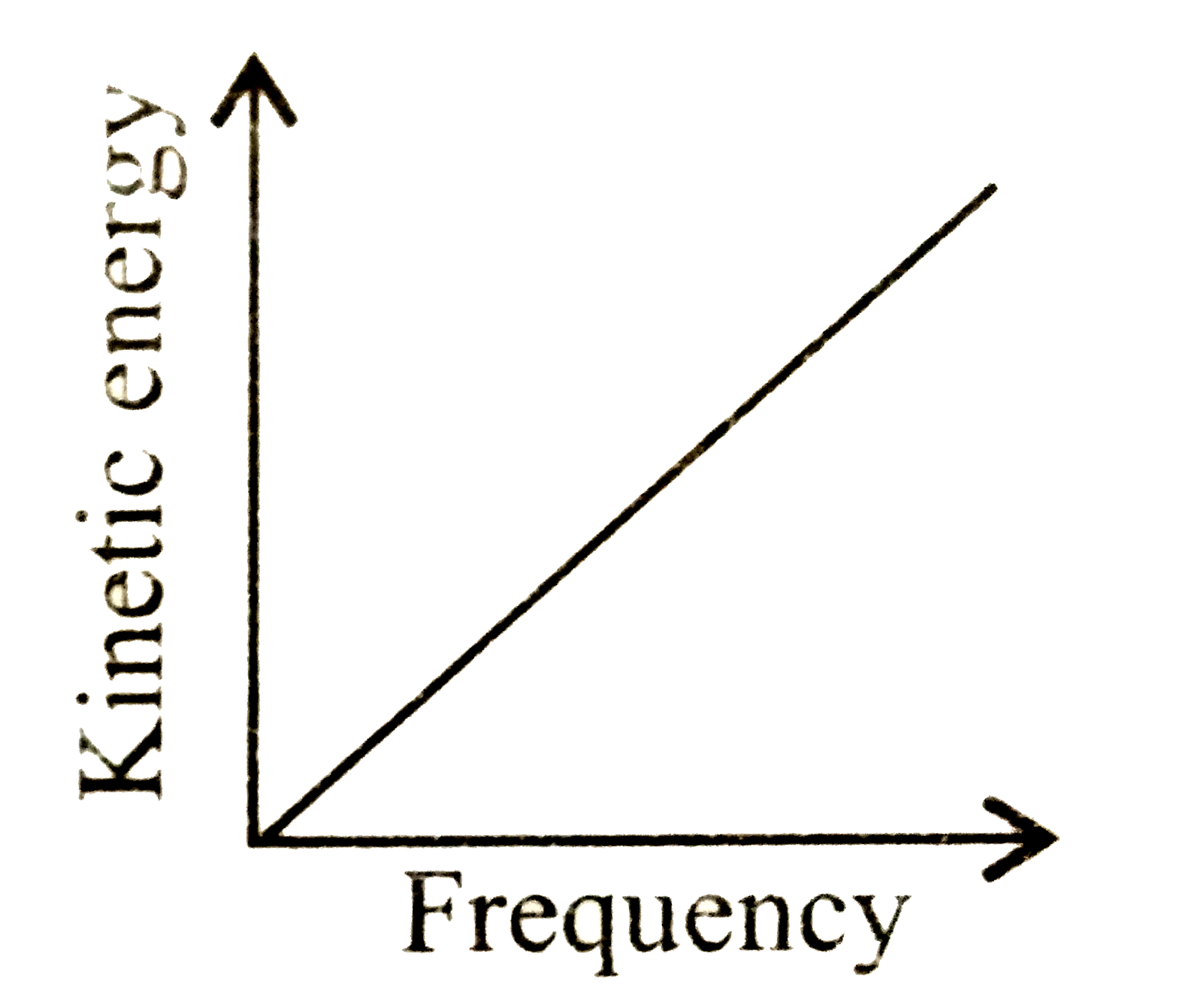 D
D
By photoelectric effect, Einstein, proved
View SolutionAccording to Einstein's photoelectric equation (symbols have their usual meaning)
View SolutionWrite six salient features of genetic code
View SolutionWrite ideal gas equation.
View SolutionWrite any three uses of PCR
View SolutionWhat is photoelectric effect? Mention the Einstein's photoelectric equation.
View SolutionWrite Einstein's photoelectric equation and point out any two characteristic properties of photons on which this equation is based.
View Solution

