Find the relation between drift velocity and relaxation time of charge carriers in a conductor .
A conductor of length L is connected to a d.c source of emf 'E' . If the length of the conductor is tripled by stetching it, keeping 'E' constant , explain how its drift velocity would be affected.
To find the relation between drift velocity and relaxation time of charge carriers in a conductor, we can start with the definitions and relationships involved in the motion of charge carriers under an electric field.
1. Understanding Drift Velocity (Vd):
The drift velocity (Vd) of charge carriers in a conductor is given by the formula:
Vd=A⋅t
where A is the acceleration of the charge carriers and t is the relaxation time.
2. Acceleration of Charge Carriers:
The acceleration A of charge carriers can be expressed as:
A=eEm
where:
- e is the charge of the electron,
- E is the electric field,
- m is the mass of the electron.
3. Substituting Acceleration into Drift Velocity:
By substituting A into the drift velocity equation, we get:
Vd=eEm⋅t
4. Current in the Conductor:
The current I in the conductor can be expressed as:
I=nAVd
where n is the number density of charge carriers and A is the cross-sectional area of the conductor.
5. Relating Current to Resistance:
Ohm's law states that:
I=ER
where R is the resistance of the conductor.
6. Resistance and Length:
The resistance R of a conductor is given by:
R=ρLA
where ρ is the resistivity of the material, L is the length, and A is the cross-sectional area.
7. Effect of Tripling Length:
If the length L of the conductor is tripled while keeping the electric field E constant, the new resistance R′ becomes:
R′=ρ3LA=3R
Thus, the resistance increases by a factor of 3.
8. Finding New Drift Velocity:
Since I=ER, if R increases, the current I decreases. The new drift velocity V′d can be expressed as:
V′d=InA
Since the current decreases due to increased resistance, we can relate the new drift velocity to the original drift velocity:
V′d=Vd3
Therefore, the new drift velocity is one-third of the original drift velocity.
Conclusion:
The relation between drift velocity Vd and relaxation time t is given by:
Vd=eEm⋅t
When the length of the conductor is tripled, the drift velocity decreases to one-third of its original value.
The drift velocity (Vd) of charge carriers in a conductor is given by the formula:
Vd=A⋅t
where A is the acceleration of the charge carriers and t is the relaxation time.
The acceleration A of charge carriers can be expressed as:
A=eEm
where:
- e is the charge of the electron,
- E is the electric field,
- m is the mass of the electron.
By substituting A into the drift velocity equation, we get:
Vd=eEm⋅t
The current I in the conductor can be expressed as:
I=nAVd
where n is the number density of charge carriers and A is the cross-sectional area of the conductor.
Ohm's law states that:
I=ER
where R is the resistance of the conductor.
The resistance R of a conductor is given by:
R=ρLA
where ρ is the resistivity of the material, L is the length, and A is the cross-sectional area.
If the length L of the conductor is tripled while keeping the electric field E constant, the new resistance R′ becomes:
R′=ρ3LA=3R
Thus, the resistance increases by a factor of 3.
Since I=ER, if R increases, the current I decreases. The new drift velocity V′d can be expressed as:
V′d=InA
Since the current decreases due to increased resistance, we can relate the new drift velocity to the original drift velocity:
V′d=Vd3
Therefore, the new drift velocity is one-third of the original drift velocity.
The relation between drift velocity Vd and relaxation time t is given by:
Vd=eEm⋅t
When the length of the conductor is tripled, the drift velocity decreases to one-third of its original value.
Similar Questions
Define drift velocity and relaxation time, with reference to the free electron theory of conductors.
View Solution(a) Using Ampere.s circuital law or Biot Savart.s law, show that magnetic flux density .B. at a point P at a perpendicular distance.d from a long current carrying conductor is given by: B=(μ04π)2Ia (Statement of the law is not required)
(b) Define the terms (i) drift velocity, (ii) relaxation time. A conductor of length L is connected to a d.c. source of emf E. If this conductor is replaced by another conductor of same material and same area of cross-section but of length 3L, how will the drift velocity change?
View SolutionA conductor of length L is connected to a dc source of emf ε. If this conductor is replaced by another conductor of same material and same area of cross-section but of length 3L, how will the drift velocity change?
View SolutionConsider a conductor of length 40 cm where a potential difference of 10V is maintained between the ends of the conductor. Find the mobility of the electrons provided the drift velocity of the electrons is 5×10−6ms−1
View SolutionThe drift velocity of free electrons in a conductor of length 6 m is 0.25 ms−1 under the application of potential difference of 100 V. The mobility of free electrons is
View SolutionDerive the expression for drift velocity of free electron in terms of relaxation time and electric field applied across a conductor.
View SolutionDerive the expression for drift velocity of free electron in terms of relaxation time and electric field applied across a conductor.
View SolutionA straight conductor of uniform cross section carries a time varying current, which varies at the rate dI//dt = I. If s is the specific charge that is carried by each charge carries of the conductor and l is the length of the condcutor, then the totalt force experienced by all the charge carries per unit length of the conductor due to their drift velocities only is
View SolutionHow does the mobility of electrons in a conductor change, if the p.d. applied across the conductor is doubled, keeping its length and temperature constant?
View SolutionFigure shows a conical conducting wire connected to a source of emf. Let E, vd, I represent the electric field, drift velocity and current at a cross-section of the wire. As one moves from end A to B of the wire
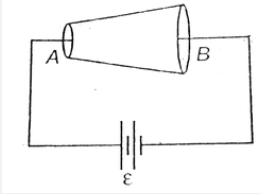
View Solution
