Answer the following:
(i) If two similar large plates, each of area A having surface charge densities +σ and −σ are separated by a distance d in air,find the expression for
(a) field at points between the two plates and on outer side of the plates. Specify the direction of the field in each case.
(b) the potential difference between the plates.
(c) the capacitance of the capacitor so formed.
(ii) Two metallic spheres of radii R and 2R are charged so that both of these have same surface charge density σ. If they are connected to each other with a conducting wire, in which direction will the charge flow and why ?
Let's break down the solution step by step:
(i) Two large plates with surface charge densities +σ and -σ
(a) Electric Field at Points Between and Outside the Plates
1. Electric Field Outside the Plates:
- For the region outside the positively charged plate (+σ), the electric field E1 is given by:
E1=σ2ϵ0
- For the region outside the negatively charged plate (-σ), the electric field E2 is given by:
E2=−σ2ϵ0
- Therefore, the total electric field outside both plates (either side) is:
E=E1+E2=σ2ϵ0−σ2ϵ0=0
- Direction: The electric field is zero outside both plates.
2. Electric Field Between the Plates:
- Inside the plates, the electric fields add up:
E=σ2ϵ0+σ2ϵ0=σϵ0
- Direction: The electric field direction is from the positive plate to the negative plate.
(b) Potential Difference Between the Plates
- The potential difference V between the plates can be calculated using the formula:
V=E⋅d
- Substituting the electric field between the plates:
V=(σϵ0)⋅d
(c) Capacitance of the Capacitor Formed
- The capacitance C is defined as:
C=QV
- Where Q is the charge on one plate, which can be expressed as Q=σA.
- Substituting V:
C=σA(σϵ0)d=ϵ0Ad
(ii) Charge Flow Between Two Metallic Spheres
1. Given: Two metallic spheres of radii R and 2R are charged with the same surface charge density σ.
2. Potential Calculation:
- The potential V on the surface of a sphere is given by:
V=14πϵ0⋅QR
- For sphere of radius R:
V1=14πϵ0⋅Q1R
- For sphere of radius 2R:
V2=14πϵ0⋅Q22R
- Since both spheres have the same surface charge density σ:
Q1=σ⋅4πR2andQ2=σ⋅4π(2R)2=4σ⋅4πR2
- Therefore, substituting these into the potential equations:
V1=σ⋅4πR24πϵ0R=σRϵ0
V2=4σ⋅4πR24πϵ0⋅2R=2σRϵ0
3. Direction of Charge Flow:
- Since V1>V2, charge will flow from the sphere with radius R (higher potential) to the sphere with radius 2R (lower potential).
Summary of Answers:
- (a) Electric field outside both plates is 0; between the plates is σϵ0 directed from +σ to -σ.
- (b) Potential difference V=σdϵ0.
- (c) Capacitance C=ϵ0Ad.
- (ii) Charge flows from the sphere of radius R to the sphere of radius 2R.
- For the region outside the positively charged plate (+σ), the electric field E1 is given by:
E1=σ2ϵ0
- For the region outside the negatively charged plate (-σ), the electric field E2 is given by:
E2=−σ2ϵ0
- Therefore, the total electric field outside both plates (either side) is:
E=E1+E2=σ2ϵ0−σ2ϵ0=0
- Direction: The electric field is zero outside both plates.
- Inside the plates, the electric fields add up:
E=σ2ϵ0+σ2ϵ0=σϵ0
- Direction: The electric field direction is from the positive plate to the negative plate.
V=E⋅d
- Substituting the electric field between the plates:
V=(σϵ0)⋅d
C=QV
- Where Q is the charge on one plate, which can be expressed as Q=σA.
- Substituting V:
C=σA(σϵ0)d=ϵ0Ad
2. Potential Calculation:
- The potential V on the surface of a sphere is given by:
V=14πϵ0⋅QR
- For sphere of radius R:
V1=14πϵ0⋅Q1R
- For sphere of radius 2R:
V2=14πϵ0⋅Q22R
- Since both spheres have the same surface charge density σ:
Q1=σ⋅4πR2andQ2=σ⋅4π(2R)2=4σ⋅4πR2
- Therefore, substituting these into the potential equations:
V1=σ⋅4πR24πϵ0R=σRϵ0
V2=4σ⋅4πR24πϵ0⋅2R=2σRϵ0
3. Direction of Charge Flow:
- Since V1>V2, charge will flow from the sphere with radius R (higher potential) to the sphere with radius 2R (lower potential).
- (a) Electric field outside both plates is 0; between the plates is σϵ0 directed from +σ to -σ.
- (b) Potential difference V=σdϵ0.
- (c) Capacitance C=ϵ0Ad.
- (ii) Charge flows from the sphere of radius R to the sphere of radius 2R.
Topper's Solved these Questions
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SECTION-D
Explore 15 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:SET-I (SECTION-A)
Explore 4 Videos
- XII BOARDSBook:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:XII BOARDSExercise:Section -C
Explore 7 Videos
- SAMPLE PAPER 2019Book:XII BOARD PREVIOUS YEAR PAPER ENGLISHChapter:SAMPLE PAPER 2019Exercise:SECTION D
Explore 6 Videos
Similar Questions
The force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
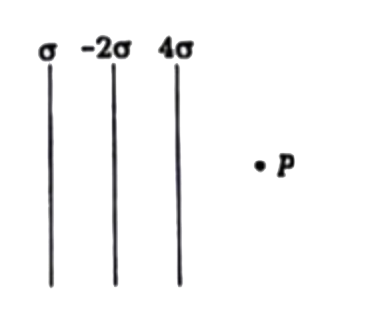
View SolutionThree non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
View SolutionTwo thin infinite parallel plates have uniform charge densities +σ and −σ. The electric field in the space between them is
View SolutionCharges 2q and −3q are given to two identical metal plates of area of cross section A. the distance between the plates is d. Find the capacitance and potential difference between the plates.
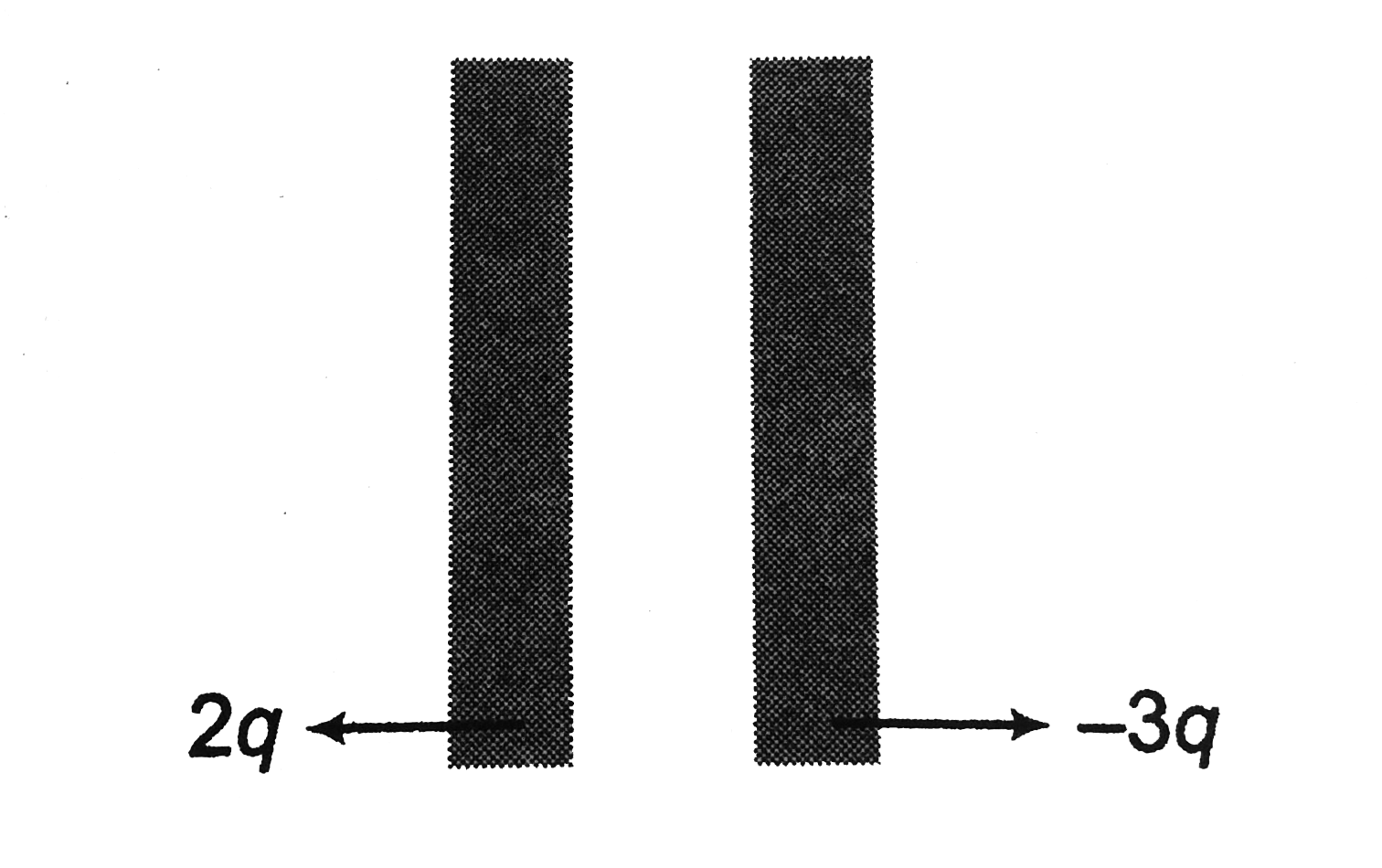
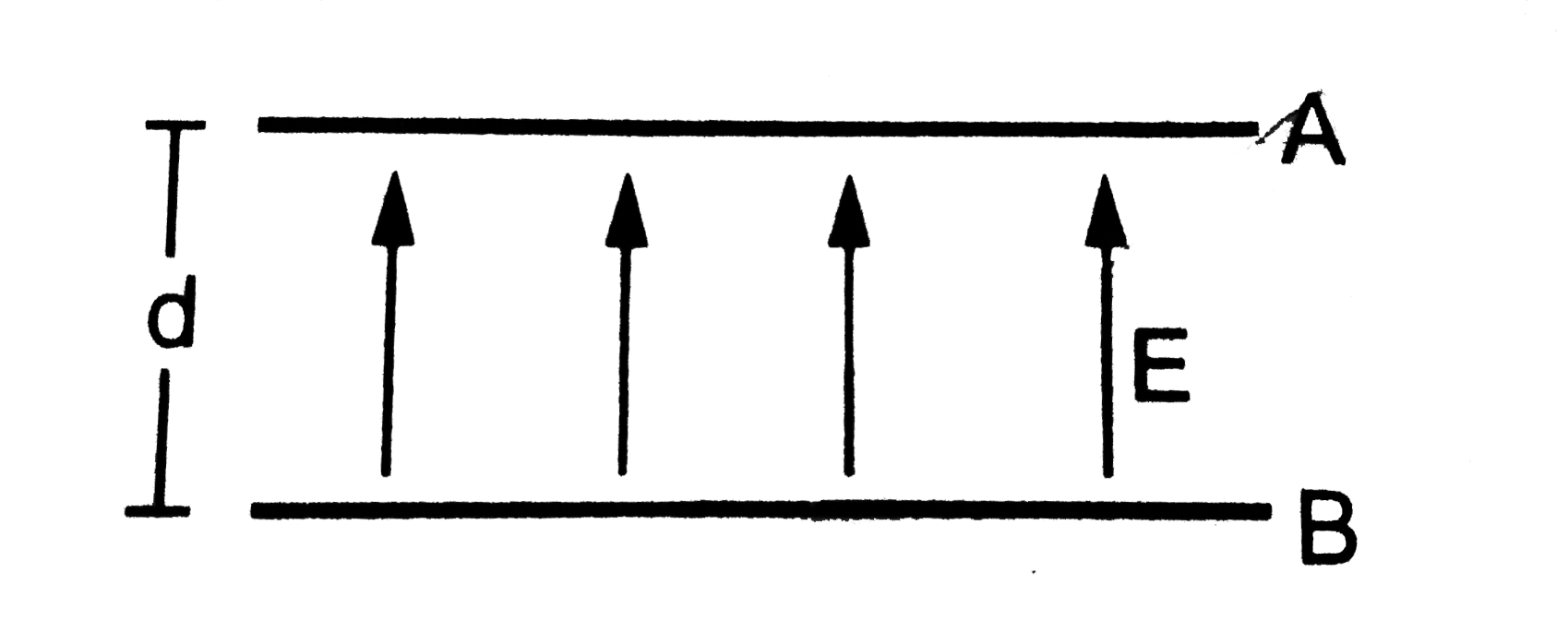
View SolutionFigure shows two metallic plates A and B placed parallel to each other at a seperation d. A uniform electric field E exists between the plates in the direction from plate B to plate A. Find the potential difference between the plates.
View SolutionThe plates of a parallel-plate capacior are given equal positive charges .What will be the potential difference between the plates ? What will be the charges on the facing surfaces and on the outer surfaces ?
View SolutionFind potential difference across the plates AB if capacitance between the plates is C and area of each plate is equal and Q1,Q2(<Q1) are charges given to the plates
View SolutionSeparation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
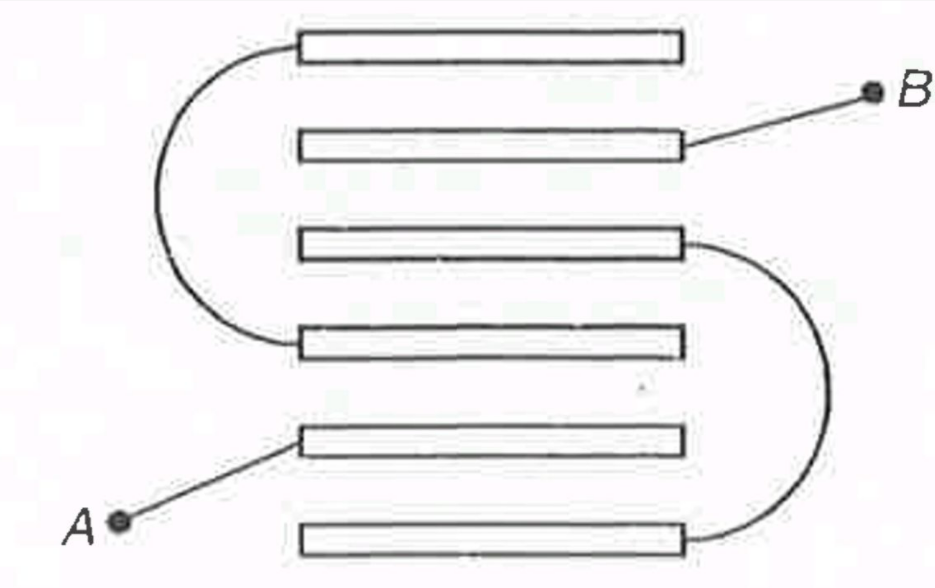
View SolutionPlates of area A are arranged as shown. The distance between each plate is d , the net capacitance is
View SolutionTwo parallel conducting plates of a capacitor of capacitance C containing charges Q and -2Q at a distance d apart. Find out potential difference between the plates of capacitors.
View Solution
