(a) Draw a plot showing the variation of potential energy of a pair of nucleons as a function of their separation . Mark the regions where the nuclear force is :
(i) attractive and (ii) repulsive.
(b) In the nuclear reaction
n+235U→92aXe+54 94Sr+2nb determine the values of a and b .
Step-by-Step Solution
1. Understanding the Concept:
- The potential energy of a pair of nucleons (neutrons and protons) varies with their separation distance.
- At very short distances (less than 1 femtometer), the nuclear force is repulsive due to the strong interaction between nucleons.
- Beyond this distance, the force becomes attractive, leading to a decrease in potential energy.
2. Drawing the Graph:
- Draw a graph with the x-axis representing the separation distance (R) in femtometers (fm) and the y-axis representing potential energy (U) in mega electron volts (MeV).
- Mark the x-axis with values starting from 0 fm, and label the negative potential energy values down to -100 MeV.
3. Plotting the Regions:
- For distances less than 1 fm, draw a curve that rises steeply towards the positive potential energy region, indicating repulsion.
- At 1 fm, the curve should drop sharply into the negative region, indicating the onset of attraction.
- As the separation increases beyond 1 fm, the potential energy continues to decrease, indicating stronger attraction until it levels off.
4. Labeling the Regions:
- Clearly label the area where the force is repulsive (for R < 1 fm) and the area where the force is attractive (for R > 1 fm).
Part (b): Determining Values of A and B in the Nuclear Reaction
1. Understanding the Reaction:
- The nuclear reaction is given as:
n+23592U→a54Xe+94bSr+2n
- Here, we need to conserve both atomic numbers and mass numbers.
2. Conserving Atomic Numbers:
- The atomic number on the left side is:
0+92=92
- The atomic number on the right side is:
54+B+2×0=54+B
- Setting these equal gives:
92=54+B⟹B=92−54=38
3. Conserving Mass Numbers:
- The mass number on the left side is:
1+235=236
- The mass number on the right side is:
A+94+2×1=A+94+2=A+96
- Setting these equal gives:
236=A+96⟹A=236−96=140
4. Final Values:
- The values determined are:
- A=140
- B=38
Final Answers:
- Part (a): The graph shows potential energy vs. separation with regions marked for attractive and repulsive forces.
- Part (b): A=140 and B=38.
- The potential energy of a pair of nucleons (neutrons and protons) varies with their separation distance.
- At very short distances (less than 1 femtometer), the nuclear force is repulsive due to the strong interaction between nucleons.
- Beyond this distance, the force becomes attractive, leading to a decrease in potential energy.
- Draw a graph with the x-axis representing the separation distance (R) in femtometers (fm) and the y-axis representing potential energy (U) in mega electron volts (MeV).
- Mark the x-axis with values starting from 0 fm, and label the negative potential energy values down to -100 MeV.
- For distances less than 1 fm, draw a curve that rises steeply towards the positive potential energy region, indicating repulsion.
- At 1 fm, the curve should drop sharply into the negative region, indicating the onset of attraction.
- As the separation increases beyond 1 fm, the potential energy continues to decrease, indicating stronger attraction until it levels off.
- Clearly label the area where the force is repulsive (for R < 1 fm) and the area where the force is attractive (for R > 1 fm).
- The nuclear reaction is given as:
n+23592U→a54Xe+94bSr+2n
- Here, we need to conserve both atomic numbers and mass numbers.
- The atomic number on the left side is:
0+92=92
- The atomic number on the right side is:
54+B+2×0=54+B
- Setting these equal gives:
92=54+B⟹B=92−54=38
- The mass number on the left side is:
1+235=236
- The mass number on the right side is:
A+94+2×1=A+94+2=A+96
- Setting these equal gives:
236=A+96⟹A=236−96=140
- The values determined are:
- A=140
- B=38
- Part (a): The graph shows potential energy vs. separation with regions marked for attractive and repulsive forces.
- Part (b): A=140 and B=38.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - D
3 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION - E
5 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET -III, OUTSIDE DELHI]
3 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Draw a plot of potential energy of a pair of nucleons as a function of their separations. Mark the regions where the nuclear force is (i) attractive and (ii) repulsive. Write any two characteristic features of nuclear forces.
View SolutionDraw a plot of potential energy of a pair of nucleons as a function of their separation . Write two important conclusions which you can draw regarding the nature of nuclear forces .
View SolutionAre strong nuclear forces basically attractive?
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,
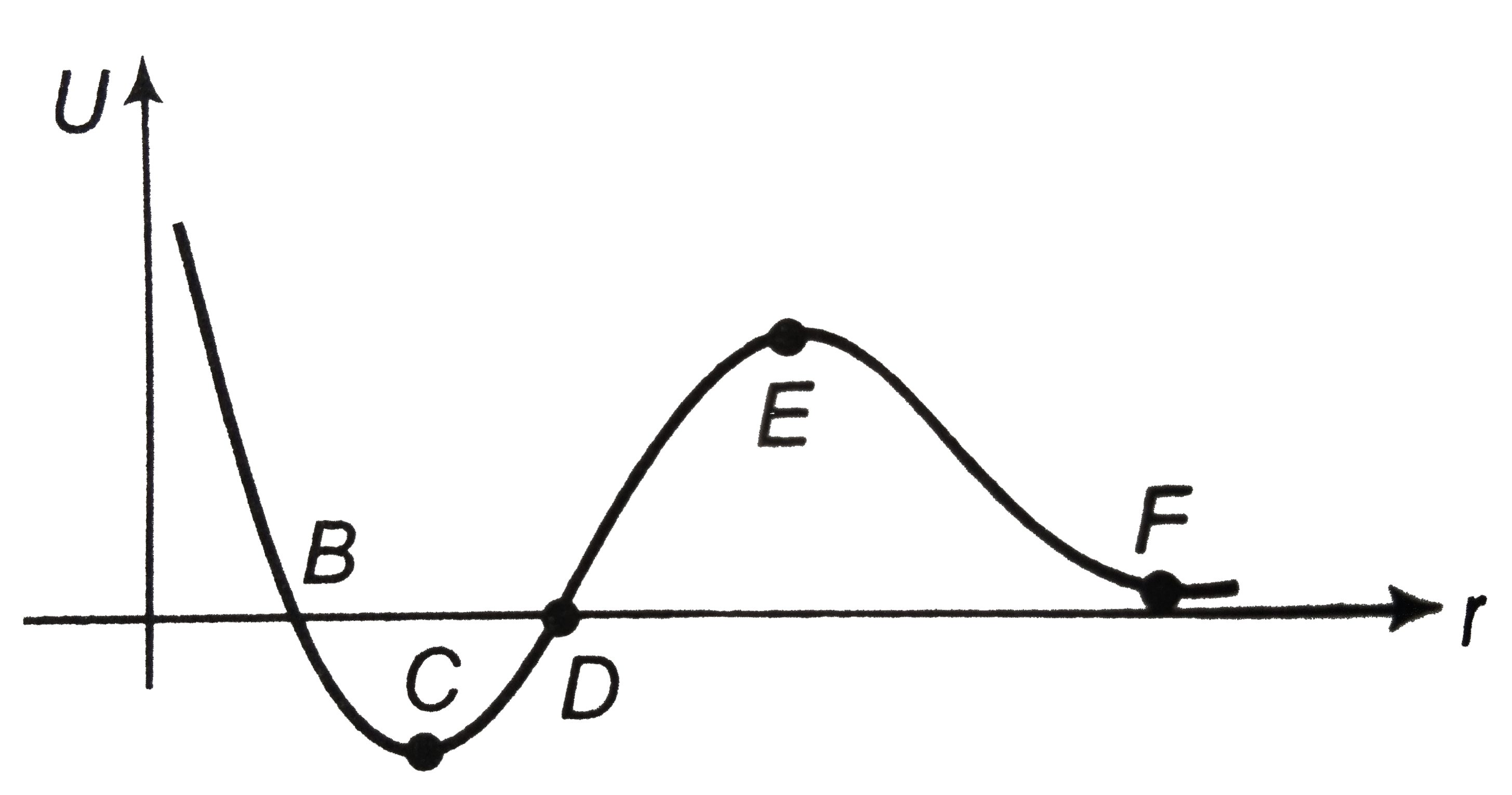
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,

View SolutionThe curve in the diagram shows a potential energy U of two molecules for different values of intermolecular separation r. Which part of the curve represent that the intermolecular force is (i) repulsive, (ii) attractive ?
View SolutionDraw a plot showing the variation of (i) electric field (E ) and (ii) electric potential (V) with distance r due to a point charge Q.
View SolutionIn
−NO2(i),−NH2(ii),−SO3H(iii) ,
The decreasing order of -I effect is
View SolutionNuclear energy is released in fusion reaction, since binding energy per nucleon is
View SolutionThe nuclear force between two nucleons is explained by
View Solution
