Questions on Sector
To find the area of a sector given its radius and the angle subtended at the center, we can follow these steps:
1. Identify the given values:
- Radius r=7 cm
- Angle θ=90∘
2. Use the formula for the area of a sector:
The area A of a sector can be calculated using the formula:
A=θ360×πr2
3. Substitute the known values into the formula:
- Substitute θ=90∘ and r=7 cm into the formula:
A=90360×π×(7)2
4. Simplify the fraction:
- The fraction 90360 simplifies to 14:
A=14×π×(7)2
5. Calculate r2:
- Calculate 72=49:
A=14×π×49
6. Substitute the value of π:
- Use π≈227:
A=14×227×49
7. Perform the multiplication:
- 49÷7=7:
A=14×22×7
8. Calculate the final area:
- Multiply 22×7=154:
A=1544 cm2
- Simplifying 1544 gives 38.5 cm2.
Final Answer
The area of the sector is 38.5 cm2.
- Radius r=7 cm
- Angle θ=90∘
The area A of a sector can be calculated using the formula:
A=θ360×πr2
- Substitute θ=90∘ and r=7 cm into the formula:
A=90360×π×(7)2
- The fraction 90360 simplifies to 14:
A=14×π×(7)2
- Calculate 72=49:
A=14×π×49
- Use π≈227:
A=14×227×49
- 49÷7=7:
A=14×22×7
- Multiply 22×7=154:
A=1544 cm2
- Simplifying 1544 gives 38.5 cm2.
The area of the sector is 38.5 cm2.
Similar Questions
Figure shows a sector of a circle of radius r containing an angle θ∘ The area of the sector is Acm2 and the perimeter is 50cm. Prove that θ=360π(25r−1) and A=25r−r2
View SolutionIf you have a spinning wheel with 3-green sectors, 1-blue sector and 1-red sector. What is the probability of getting a green sector? Is it the maximum?
View SolutionIf the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take π=22/7 ) (FIGURE)
View SolutionThe central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120∘and40∘ . Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe ?
View SolutionFind the area of the minor segment of a circle of radius 14cm, when the angle of the corresponding sector is 60∘

View SolutionIs it true to say that area of segment of a circle is less than the area of its corresponding sector? Why ?
View SolutionThe areas of two sectors of two different circles are equal. Is it necessary that their corresponding arc lengths are equal ? Why ?
View SolutionFind the area of the segment of a circle of radius 12 cm whose corresponding sector has a central angle of 60∘ . (use π=3.14)
View SolutionThe perimeter of a certain sector of a circle is equal to half that of the circle of which it is a sector. The circular measure of one angle of the sector is
View SolutionWhat is the ratio of the areas of the major sector in diagram A to the minor sector in a diagram B?
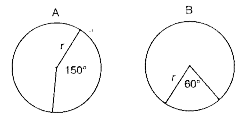
View Solution
