A cottage industry manufactures pedestal lamps and wooden shades.Both the products require machine time as well as craftsman time in the making.The number of hours required for producing 1 unit of each and the corresponding profit is given in the following table:
In a day,the factory has availability of not more than 42 hours of machine time and 24 hours of craftsman time.
Assuming that all items manufactured are sold,how should the manufacturer schedule his daily production in order to maximise the profit?Formulate it as an LPP and solve it graphically
To solve the problem of maximizing profit from the production of pedestal lamps and wooden shades using Linear Programming, we will follow these steps:
Step 1: Define the Variables
Let:
- x = number of pedestal lamps produced
- y = number of wooden shades produced
Step 2: Formulate the Objective Function
The profit from each pedestal lamp is 30 and from each wooden shade is 20. Therefore, the objective function to maximize profit Z is:
Z=30x+20y
Step 3: Formulate the Constraints
From the problem statement, we have the following constraints based on machine time and craftsman time:
1. Machine time constraint:
1.5x+3y≤42
2. Craftsman time constraint:
3x+y≤24
3. Non-negativity constraints:
x≥0,y≥0
Step 4: Graph the Constraints
To graph the constraints, we will convert the inequalities into equations and find the intercepts.
1. For the machine time constraint 1.5x+3y=42:
- When x=0:
3y=42⟹y=14(Point: (0, 14))
- When y=0:
1.5x=42⟹x=28(Point: (28, 0))
2. For the craftsman time constraint 3x+y=24:
- When x=0:
y=24(Point: (0, 24))
- When y=0:
3x=24⟹x=8(Point: (8, 0))
Step 5: Identify the Feasible Region
Plot the points (0, 14), (28, 0), (0, 24), and (8, 0) on a graph. The feasible region is where the constraints overlap, which is in the first quadrant (since x and y must be non-negative).
Step 6: Find the Intersection of the Constraints
To find the intersection of the lines 1.5x+3y=42 and 3x+y=24, we can solve the equations simultaneously.
1. Multiply the second equation by 3:
9x+3y=72
2. Now subtract the first equation from this:
(9x+3y)−(1.5x+3y)=72−42
7.5x=30⟹x=4
3. Substitute x=4 back into one of the original equations to find y:
3(4)+y=24⟹12+y=24⟹y=12
- So, the intersection point is (4,12).
Step 7: Evaluate the Objective Function at the Corner Points
The corner points of the feasible region are:
1. (0,14)
2. (8,0)
3. (4,12)
Calculate Z at each corner point:
1. At (0,14):
Z=30(0)+20(14)=280
2. At (8,0):
Z=30(8)+20(0)=240
3. At (4,12):
Z=30(4)+20(12)=120+240=360
Step 8: Determine the Maximum Profit
The maximum profit occurs at the point (4,12) with a profit of 360.
Final Answer
To maximize profit, the manufacturer should produce:
- 4 pedestal lamps
- 12 wooden shades
Let:
- x = number of pedestal lamps produced
- y = number of wooden shades produced
The profit from each pedestal lamp is 30 and from each wooden shade is 20. Therefore, the objective function to maximize profit Z is:
Z=30x+20y
From the problem statement, we have the following constraints based on machine time and craftsman time:
1. Machine time constraint:
1.5x+3y≤42
2. Craftsman time constraint:
3x+y≤24
3. Non-negativity constraints:
x≥0,y≥0
To graph the constraints, we will convert the inequalities into equations and find the intercepts.
- When x=0:
3y=42⟹y=14(Point: (0, 14))
- When y=0:
1.5x=42⟹x=28(Point: (28, 0))
- When x=0:
y=24(Point: (0, 24))
- When y=0:
3x=24⟹x=8(Point: (8, 0))
Plot the points (0, 14), (28, 0), (0, 24), and (8, 0) on a graph. The feasible region is where the constraints overlap, which is in the first quadrant (since x and y must be non-negative).
To find the intersection of the lines 1.5x+3y=42 and 3x+y=24, we can solve the equations simultaneously.
9x+3y=72
(9x+3y)−(1.5x+3y)=72−42
7.5x=30⟹x=4
3(4)+y=24⟹12+y=24⟹y=12
- So, the intersection point is (4,12).
The corner points of the feasible region are:
1. (0,14)
2. (8,0)
3. (4,12)
1. At (0,14):
Z=30(0)+20(14)=280
2. At (8,0):
Z=30(8)+20(0)=240
3. At (4,12):
Z=30(4)+20(12)=120+240=360
The maximum profit occurs at the point (4,12) with a profit of 360.
To maximize profit, the manufacturer should produce:
- 4 pedestal lamps
- 12 wooden shades
Topper's Solved these Questions
Similar Questions
A cottage industry manufactures pedestal lamps and wooden shades.Both the products require machine time as well as craftsman time in the making. The number of hours required for producing 1unit of each and the corresponding profit is given in the following table : In a day, the factory has availability of not more than 42 hours of machine time and 24 hours of craftsman time, Assuming that all items manufactured manufacturer schedule his daily production in order to maximize profit ? Formulate it as an LPP and solve it graphically.

View SolutionA factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftmans time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftmans time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsmans time. If the profit on a racket and on a bat is Rs. 20 and Rs. 10 respectively, find the number of tennis rackets and crickets bats that the factory must manufacture to earn the maximum profit. Make it as an L.P.P. and solve graphically.
View Solution
Knowledge Check
A 24 - hour day is how many times as long as 60 seconds ?
A12B30C365D1,440
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 25 and that from a shade is Rs. 15. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit. Formulate an LPP and solve it graphically.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes one hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Make an L.P.P. and solve it graphically.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes one hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Make an L.P.P. and solve it graphically.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B, each type requiring the use of two machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on hand-operated machines to manufacture a packet of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machines to manufacture a packet of screws 'B'. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a packet of screws 'A' at a profit of 70 paise and screws 'B' at a profit of Rs. 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximise his profit ? Formulate the above L.P.P. and solve it graphically and find the maximum profit.
View SolutionA company uses three machines to manufacture two types of shirts, half sleeves and full sleeves. The number of hours required per week on machine M1,M2andM3 for one shirt of each type is given in the following table :
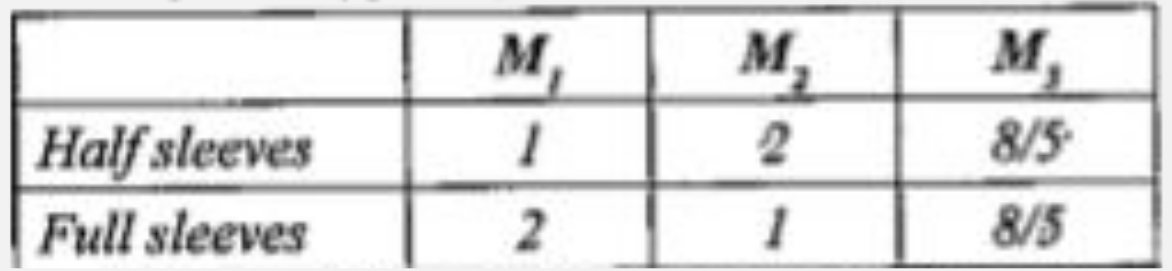
None of the machines can be in operation for more than 40 hours per week. The profit on each half sleeve shirt is Rs 1 and the profit on each full sleeve shirt is Rs 1.50. How many of each type of shirts should be made per week to maximize the company's profit ?
View Solution
