The mean of the following distribution is 18. Find the frequency f of the class 19−21.
To find the frequency f of the class 19−21 given that the mean of the distribution is 18, we will follow these steps:
Step 1: Identify the mid-values of the classes
The classes given are:
- 11−13
- 13−15
- 15−17
- 17−19
- 19−21 (frequency f is unknown)
- 21−23
- 23−25
The mid-values xi for each class can be calculated as follows:
- For 11−13: x1=11+132=12
- For 13−15: x2=13+152=14
- For 15−17: x3=15+172=16
- For 17−19: x4=17+192=18
- For 19−21: x5=19+212=20
- For 21−23: x6=21+232=22
- For 23−25: x7=23+252=24
Step 2: Calculate fixi for each class
Assuming the frequencies for the classes are:
- f1=4 (for 11−13)
- f2=6 (for 13−15)
- f3=8 (for 15−17)
- f4=10 (for 17−19)
- f5=f (for 19−21)
- f6=6 (for 21−23)
- f7=4 (for 23−25)
Now, we calculate fixi:
- f1x1=4×12=48
- f2x2=6×14=84
- f3x3=8×16=128
- f4x4=10×18=180
- f5x5=f×20=20f
- f6x6=6×22=132
- f7x7=4×24=96
Step 3: Calculate the summations
Now, we find the total of fixi and fi:
- Σfixi=48+84+128+180+20f+132+96=668+20f
- Σfi=4+6+8+10+f+6+4=38+f
Step 4: Set up the equation for the mean
Given that the mean is 18:
ΣfixiΣfi=18
Substituting the summations:
668+20f38+f=18
Step 5: Cross-multiply and simplify
Cross-multiplying gives:
668+20f=18(38+f)
Expanding the right side:
668+20f=684+18f
Rearranging the equation:
668−684+20f−18f=0
2f=16
f=8
Conclusion
The frequency f of the class 19−21 is 8.
The classes given are:
- 11−13
- 13−15
- 15−17
- 17−19
- 19−21 (frequency f is unknown)
- 21−23
- 23−25
- For 11−13: x1=11+132=12
- For 13−15: x2=13+152=14
- For 15−17: x3=15+172=16
- For 17−19: x4=17+192=18
- For 19−21: x5=19+212=20
- For 21−23: x6=21+232=22
- For 23−25: x7=23+252=24
Assuming the frequencies for the classes are:
- f1=4 (for 11−13)
- f2=6 (for 13−15)
- f3=8 (for 15−17)
- f4=10 (for 17−19)
- f5=f (for 19−21)
- f6=6 (for 21−23)
- f7=4 (for 23−25)
- f1x1=4×12=48
- f2x2=6×14=84
- f3x3=8×16=128
- f4x4=10×18=180
- f5x5=f×20=20f
- f6x6=6×22=132
- f7x7=4×24=96
Now, we find the total of fixi and fi:
- Σfixi=48+84+128+180+20f+132+96=668+20f
- Σfi=4+6+8+10+f+6+4=38+f
Given that the mean is 18:
ΣfixiΣfi=18
Substituting the summations:
668+20f38+f=18
Cross-multiplying gives:
668+20f=18(38+f)
Expanding the right side:
668+20f=684+18f
Rearranging the equation:
668−684+20f−18f=0
2f=16
f=8
The frequency f of the class 19−21 is 8.
Topper's Solved these Questions
Similar Questions
Find the mean of the following distribution:
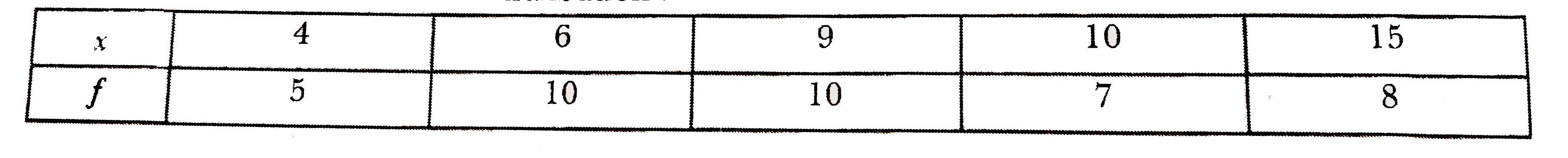
View SolutionFind the mean of the following distribution :

View SolutionFind the mean of the following distribution:

View SolutionThe mean of the following distribution is 52 and the frequency of class interval 30-40 is f. Find f.
View SolutionFind the mean for the following distribution :

View SolutionFind the mean for the following distribution :

View SolutionIf the mean of the following distribution is 7.5, find the missing frequency f

View SolutionThe mean of the following distribution is 50 but the frequency f1andf2 in classes 20-40 and 60-80, resepectively are not known. Find these frequencies, if the sum of all the fequencies is 120
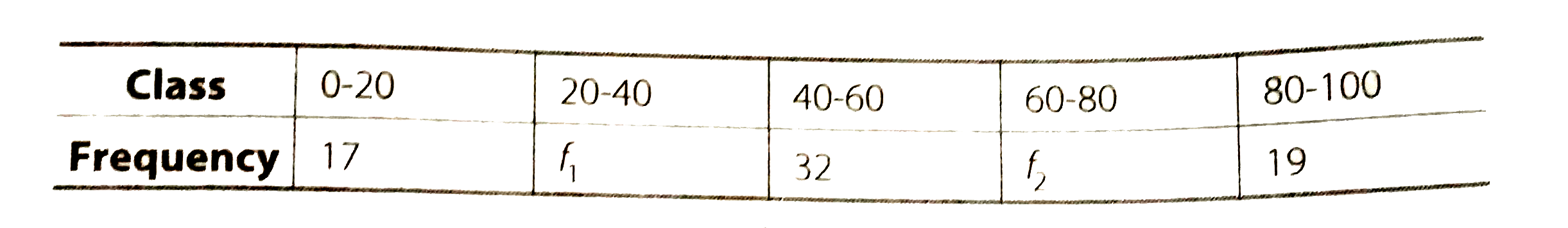
View SolutionThe mean of the following frequency distribution is 2117. Find the value of f

View SolutionThe mean of the following frequency distribution is 50. Find the value of p. Classes 0-20 20-40 40-60 60-80 80-100 Frequency 17 28 32 p 19
View Solution
