Two friends Seema and Aditya work in the same office at Delhi. In the Christmas vacations, both decided to go to their hometowns represented by Town A and Town B respectively in the figure given below. Town A and Town B are connected by trains from the same station C (in the given figure)in Delhi.Based on the given situation, answer the following questions:
img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_041_X_SQP_E03_007_Q01.png" width="80%"gt
(i) Who will travel more distance, Seema or Aditya, to reach to their hometown?
(ii) Seema and Aditya planned to meet at a location D situated at a point D represented by the mid-point of the line joining the points represented by Town A and Town B. Find the coordinates of the point represented by the point D .
(iii) Find the area of the triangle formed by joining the points represented by A, B and C.
Let's solve the problem step by step.
Step 1: Determine the distances traveled by Seema and Aditya.
Coordinates:
- Town A (A): (1, 7)
- Town B (B): (4, 2)
- Station C (C): (-4, 4)
Distance AC (Seema's distance):
Using the distance formula:
d=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and C:
AC=√((−4)−1)2+(4−7)2
Calculating:
=√(−5)2+(−3)2=√25+9=√34
Distance BC (Aditya's distance):
Using the same distance formula for B and C:
BC=√((−4)−4)2+(4−2)2
Calculating:
=√(−8)2+(2)2=√64+4=√68
Comparison:
Since √68>√34, Aditya travels more distance than Seema.
Step 2: Find the coordinates of point D (midpoint of AB).
Midpoint formula:
D=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
D=(1+42,7+22)=(52,92)
Step 3: Find the area of triangle ABC.
Area formula for triangle with vertices (x1, y1), (x2, y2), (x3, y3):
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Substituting the coordinates of A, B, and C:
Area=12|1(2−4)+4(4−7)+(−4)(7−2)|
Calculating:
=12|1(−2)+4(−3)+(−4)(5)|
=12|−2−12−20|=12|−34|=342=17
Final Answers:
(i) Aditya travels more distance than Seema.
(ii) The coordinates of point D are (52,92).
(iii) The area of triangle ABC is 17 square units.
- Town A (A): (1, 7)
- Town B (B): (4, 2)
- Station C (C): (-4, 4)
Using the distance formula:
d=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of A and C:
AC=√((−4)−1)2+(4−7)2
Calculating:
=√(−5)2+(−3)2=√25+9=√34
Using the same distance formula for B and C:
BC=√((−4)−4)2+(4−2)2
Calculating:
=√(−8)2+(2)2=√64+4=√68
Since √68>√34, Aditya travels more distance than Seema.
D=(x1+x22,y1+y22)
Substituting the coordinates of A and B:
D=(1+42,7+22)=(52,92)
Area=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Substituting the coordinates of A, B, and C:
Area=12|1(2−4)+4(4−7)+(−4)(7−2)|
Calculating:
=12|1(−2)+4(−3)+(−4)(5)|
=12|−2−12−20|=12|−34|=342=17
(i) Aditya travels more distance than Seema.
(ii) The coordinates of point D are (52,92).
(iii) The area of triangle ABC is 17 square units.
Similar Questions
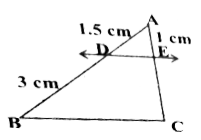
In the given fig. If DE||BC Find EC.
 View Solution
View SolutionThe equation of straight line shown in figure is :
 View Solution
View SolutionIdentify A,B,C and D,E
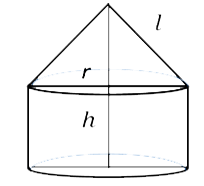
View SolutionThe total surface area of the given solid figure is _______________.
 View Solution
View SolutionAt point P, the value of dydx is :
 View Solution
View SolutionRefer the given figure and identify correct statement(s)
 View Solution
View SolutionComparison of C3andC4 plants:-
 View Solution
View SolutionWhat is the distance OA for the square shown in figure :-
 View Solution
View SolutionIf y−x=80∘ then find the values of x and y.
 View Solution
View SolutionWhat is the reading of micrometer screw gauge shown in figure
 View Solution
View Solution

