Write the relation between electric power (W ) of a device with potential differnece (Volt) across it and current ( amp ) flowing through it.
To derive the relation between electric power (W), potential difference (V), and current (I), we can follow these steps:
1. Understanding Electric Power:
- Electric power (W) is defined as the rate at which electrical energy is consumed or converted into another form of energy. It can be expressed mathematically as:
W=EnergyTime
2. Relating Power to Voltage and Current:
- The power consumed by an electrical device can also be expressed in terms of the potential difference (V) across it and the current (I) flowing through it. The formula is:
W=V×I
- Here, W is the electric power in watts (W), V is the potential difference in volts (V), and I is the current in amperes (A).
3. Using Ohm's Law:
- According to Ohm's Law, the relationship between voltage (V), current (I), and resistance (R) is given by:
V=I×R
- Rearranging this, we can express current in terms of voltage and resistance:
I=VR
4. Substituting Current in the Power Formula:
- We can substitute the expression for current (I) into the power formula:
W=V×(VR)
- This simplifies to:
W=V2R
5. Final Relations:
- Thus, we have two important relations for electric power:
W=V×IandW=V2R
Summary of the Relations:
- The relation between electric power (W), potential difference (V), and current (I) is given by:
W=V×I
- Additionally, using Ohm's Law, we can express power in terms of voltage and resistance:
W=V2R
- Electric power (W) is defined as the rate at which electrical energy is consumed or converted into another form of energy. It can be expressed mathematically as:
W=EnergyTime
- The power consumed by an electrical device can also be expressed in terms of the potential difference (V) across it and the current (I) flowing through it. The formula is:
W=V×I
- Here, W is the electric power in watts (W), V is the potential difference in volts (V), and I is the current in amperes (A).
- According to Ohm's Law, the relationship between voltage (V), current (I), and resistance (R) is given by:
V=I×R
- Rearranging this, we can express current in terms of voltage and resistance:
I=VR
- We can substitute the expression for current (I) into the power formula:
W=V×(VR)
- This simplifies to:
W=V2R
- Thus, we have two important relations for electric power:
W=V×IandW=V2R
- The relation between electric power (W), potential difference (V), and current (I) is given by:
W=V×I
- Additionally, using Ohm's Law, we can express power in terms of voltage and resistance:
W=V2R
Similar Questions
Knowledge Check
- Question 1 - Select One
A voltmeter having a resistance of 1800Ω employed to measure the potential difference across a 200Ω resistor which is connected to the terminals of a dc power supply having an emf of 50 V and an internal resistance of 20Ω. What is the percentage decrease in the potential difference across the 200Ω resistor as a result of connecting the voltmeter across it?
A1%B5%C10%D25%
If the potential difference across the ends of a conductor is doubled, the current flowing through it gets
View SolutionIn the electrical network shown in the figure, What will be the potential difference (in volt) across 3Ω resistance ?
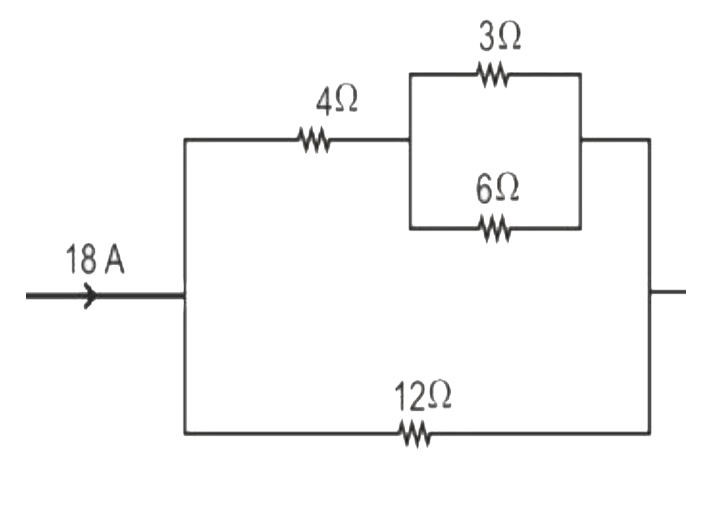 View Solution
View SolutionIn the circuit, the current flowing through 10Ω resistance is
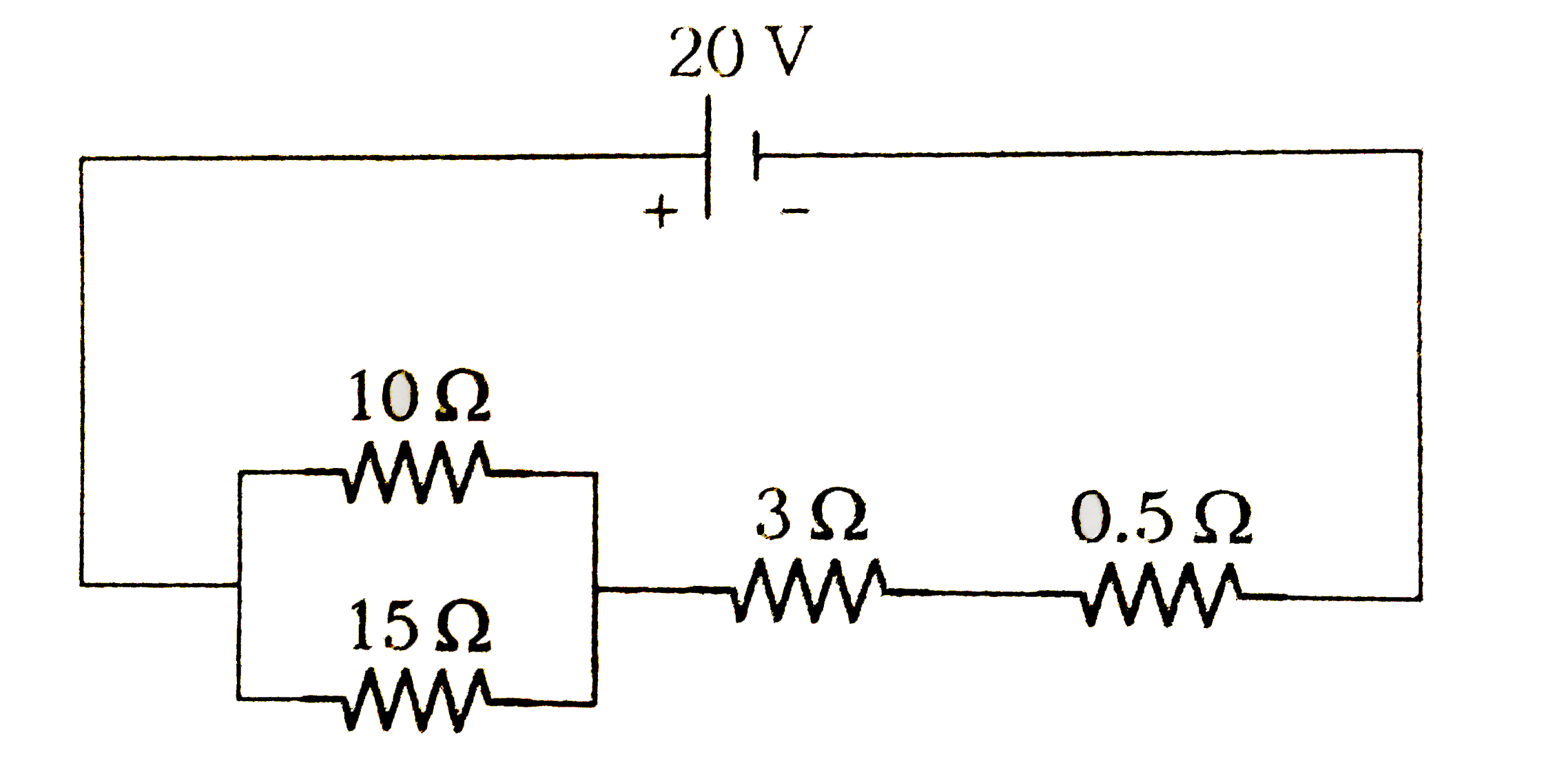 View Solution
View SolutionIn the given circuit diagram find the potential difference across 2Ω resistance (in volts).
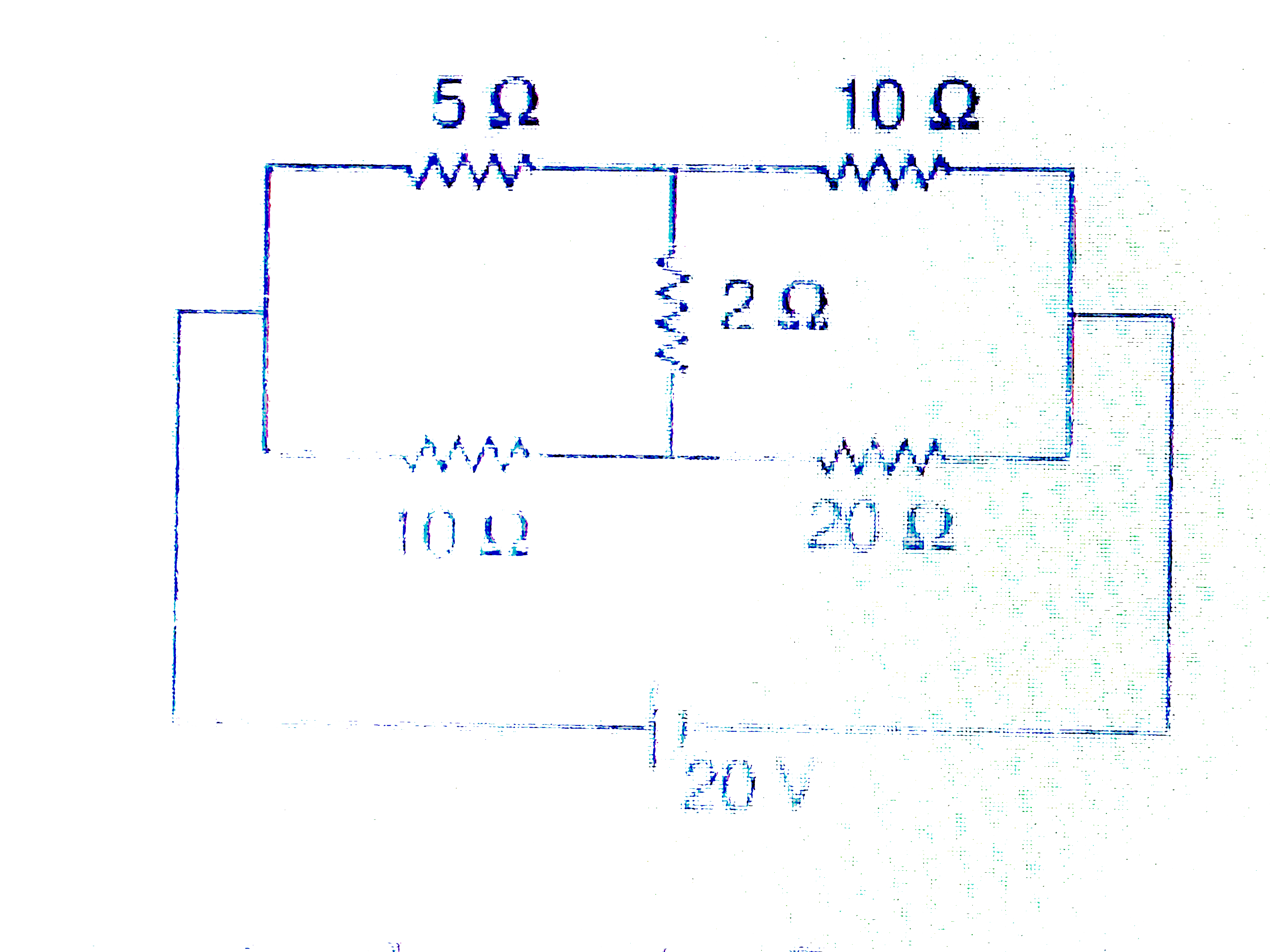 View Solution
View SolutionIn the given circuit current flowing through 2 Omega resistance is
View SolutionAlternating current flowing through a certain electrical device leads over the potential difference across it by 90∘. State whether this device is a resistor, capacitor or an inductor.
View SolutionAn electric lamp, whose resistance is 20Ω and a conductor of 4Ω resistance are connected to a 6V battery as shown in (Fig. 3.18) Calculate.
(a) the total resistance of the circuit,
(b) the current through the circuit, and
( c) the potential difference across the electric lamp and the conductor.
 .View Solution
.View Solution

