In Figure 7. find the perimeter of △ABC, if AP = 12 cm
To find the perimeter of triangle ABC given that AP = 12 cm, we can follow these steps:
Step 1: Identify the Tangents
From the problem, we know that AP and AQ are tangents to the circle from point A, and BC is also a tangent. According to the properties of tangents from an external point, the lengths of the tangents drawn from the same external point to a circle are equal.
Step 2: Set Up the Equations
Since AP = 12 cm, we can conclude that:
- AP=AQ=12cm (Equation 1)
Step 3: Identify Other Tangents
From point B, the tangents BD and BP are equal:
- BD=BP (Equation 2)
From point C, the tangents CD and CQ are equal:
- CD=CQ (Equation 3)
Step 4: Express Perimeter of Triangle ABC
The perimeter of triangle ABC can be expressed as:
Perimeter=AB+BC+AC
Step 5: Substitute for BC
Since BC is composed of the tangents from B and C:
BC=BD+CD
Thus, we can rewrite the perimeter as:
Perimeter=AB+(BD+CD)+AC
Step 6: Express AB and AC in Terms of Tangents
From the properties of tangents:
- AP=AB+BP
- AQ=AC+CQ
Substituting BP and CQ with BD and CD respectively, we have:
- AP=AB+BD (Equation 4)
- AQ=AC+CD (Equation 5)
Step 7: Substitute Equations into Perimeter
Now, substituting the expressions from Equations 4 and 5 into the perimeter equation:
Perimeter=(AP−BD)+(BD+CD)+(AQ−CD)
Step 8: Simplify the Expression
Since AP=AQ and both are equal to 12 cm:
Perimeter=(12−BD)+(BD+CD)+(12−CD)
This simplifies to:
Perimeter=12+12=24cm
Conclusion
Thus, the perimeter of triangle ABC is:
Perimeter=24cm
From the problem, we know that AP and AQ are tangents to the circle from point A, and BC is also a tangent. According to the properties of tangents from an external point, the lengths of the tangents drawn from the same external point to a circle are equal.
Since AP = 12 cm, we can conclude that:
- AP=AQ=12cm (Equation 1)
From point B, the tangents BD and BP are equal:
- BD=BP (Equation 2)
- CD=CQ (Equation 3)
The perimeter of triangle ABC can be expressed as:
Perimeter=AB+BC+AC
Since BC is composed of the tangents from B and C:
BC=BD+CD
Thus, we can rewrite the perimeter as:
Perimeter=AB+(BD+CD)+AC
From the properties of tangents:
- AP=AB+BP
- AQ=AC+CQ
- AP=AB+BD (Equation 4)
- AQ=AC+CD (Equation 5)
Now, substituting the expressions from Equations 4 and 5 into the perimeter equation:
Perimeter=(AP−BD)+(BD+CD)+(AQ−CD)
Since AP=AQ and both are equal to 12 cm:
Perimeter=(12−BD)+(BD+CD)+(12−CD)
This simplifies to:
Perimeter=12+12=24cm
Thus, the perimeter of triangle ABC is:
Perimeter=24cm
Similar Questions
In Figure , find the perimeter of ΔABC. If AP = 12 cm.
View SolutionIn the given figure find the perimeter of △ABC.
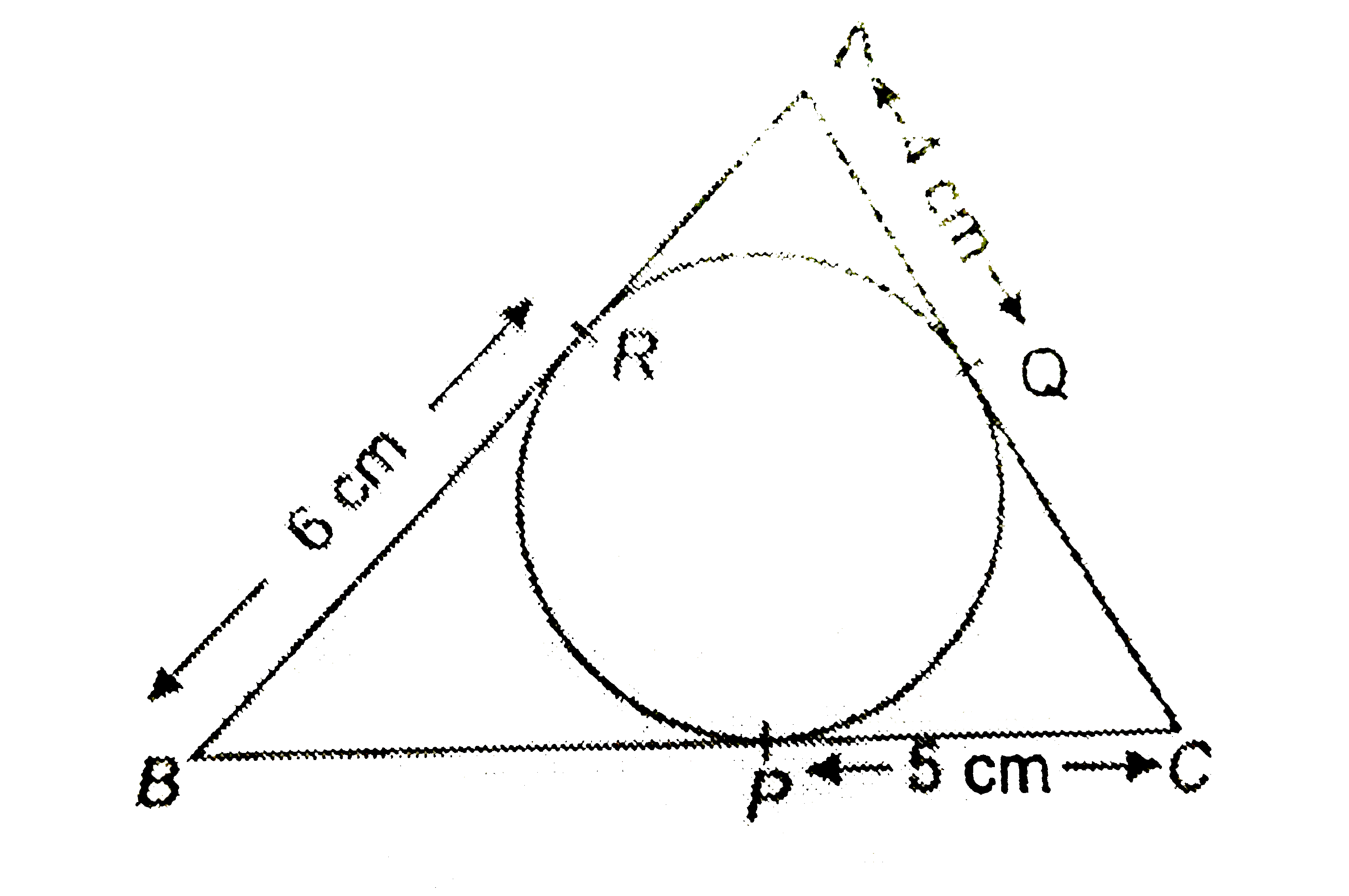
View SolutionFind the perimeter of ΔABC, if AP=12 cm

View SolutionFind the perimeter of an equilateral triangle of side 13 cm.
View SolutionFind the perimeters of the given figures.
View SolutionFind the perimeter of an equilateral triangle with side 9cm.
View SolutionFind the perimeter of the following figure:
View SolutionFind the perimeter of a hexogon of side 7 cm.
View SolutionFind the perimeter of the adjoining figure.
Given : AB = 12 cm, AC = 13 cm . DE = FG = 5 cm , EF = 10 cm and GD = 4 cm .
View SolutionIn the given figure AP and AQ are tangents to the circle with centre O. BC is tangent at point R on it.
If OA=17 cm and radius of the circle =8cm, find the perimeter of the triangle ABC.
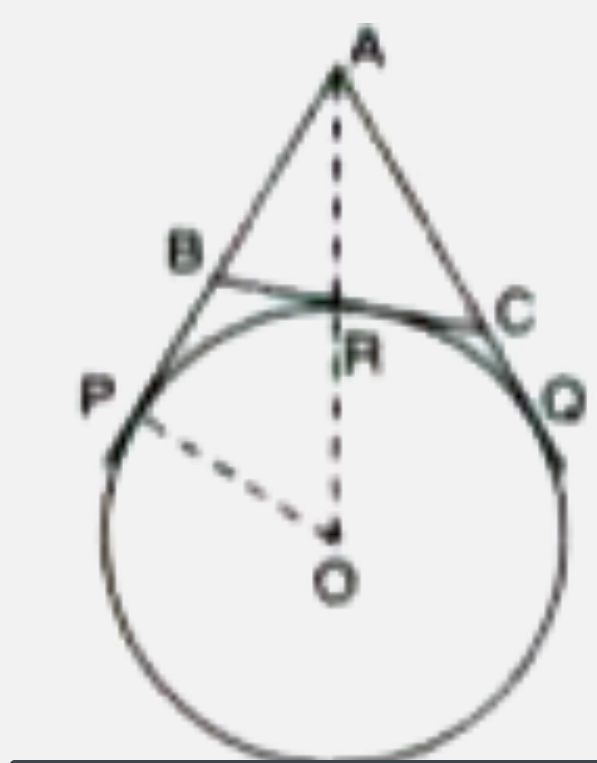
View Solution
