In figure - 3, and are shown. if AB = 3 CM, BC = 6 cm, AC = cm , = , = , XY = cm , YZ = 12 CM and XZ= 6 cm, then find the value of
To find the value of angle Y in triangles ABC and XYZ, we will follow these steps:
Step 1: Identify the given values
We have the following information:
- Triangle ABC:
- AB = 3 cm
- BC = 6 cm
- AC = 2√3 cm
- ∠A = 80°
- ∠B = 60°
- Triangle XYZ:
- XY = 4√3 cm
- YZ = 12 cm
- XZ = 6 cm
Step 2: Use the Side-Side-Side (SSS) similarity criterion
To prove that triangle ABC is similar to triangle XYZ, we will compare the ratios of their corresponding sides.
The ratios of the sides are:
- AB / XZ = 3 / 6 = 1 / 2
- AC / XY = (2√3) / (4√3) = 1 / 2
- BC / YZ = 6 / 12 = 1 / 2
Step 3: Conclude similarity
Since all the ratios of the corresponding sides are equal (1/2), we can conclude that triangle ABC is similar to triangle XYZ by the Side-Side-Side (SSS) similarity criterion.
Step 4: Relate the angles of the similar triangles
From the similarity of triangles, we have:
- ∠A = ∠X
- ∠B = ∠Z
- ∠C = ∠Y
Step 5: Calculate angle C in triangle ABC
Using the property that the sum of angles in a triangle is 180°, we can find angle C:
∠A+∠B+∠C=180°
Substituting the known values:
80°+60°+∠C=180°
∠C=180°−(80°+60°)=180°−140°=40°
Step 6: Find angle Y
Since ∠C = ∠Y (from the similarity of triangles), we have:
∠Y=∠C=40°
Final Answer
Thus, the value of angle Y is 40°.
---
We have the following information:
- Triangle ABC:
- AB = 3 cm
- BC = 6 cm
- AC = 2√3 cm
- ∠A = 80°
- ∠B = 60°
- XY = 4√3 cm
- YZ = 12 cm
- XZ = 6 cm
To prove that triangle ABC is similar to triangle XYZ, we will compare the ratios of their corresponding sides.
- AB / XZ = 3 / 6 = 1 / 2
- AC / XY = (2√3) / (4√3) = 1 / 2
- BC / YZ = 6 / 12 = 1 / 2
Since all the ratios of the corresponding sides are equal (1/2), we can conclude that triangle ABC is similar to triangle XYZ by the Side-Side-Side (SSS) similarity criterion.
From the similarity of triangles, we have:
- ∠A = ∠X
- ∠B = ∠Z
- ∠C = ∠Y
Using the property that the sum of angles in a triangle is 180°, we can find angle C:
∠A+∠B+∠C=180°
Substituting the known values:
80°+60°+∠C=180°
∠C=180°−(80°+60°)=180°−140°=40°
Since ∠C = ∠Y (from the similarity of triangles), we have:
∠Y=∠C=40°
Thus, the value of angle Y is 40°.
Similar Questions
In Figure 3,ΔABCandΔXYZ are show. If AB=3cm,BC=6cm,AC=2√3cm,∠A=80∘,∠B=60∘,XY=4√3cm,YZ=12cmandXZ=6cm, then find the value of ∠Y.
 View Solution
View SolutionIn given figure, if ∠A=∠C, AB= 6 cm, BP = 15 cm, AP = 12 cm and CP= 4 cm, then find the lengths of PD and CD.
 View Solution
View SolutionConstruct a ΔABC, when AB = 3.6 cm, BC = 3.0 cm, ∠B=30∘.
View SolutionIn ΔABC , ∠A is right - angled . If AB= 1 cm , AC =3 cm and BC = √10 cm , then find the values of cos B and sin C.
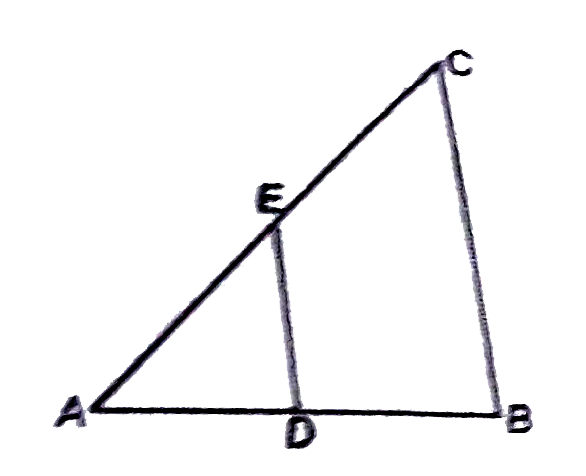
View SolutionIn the figure △ABC~△AED. If AD=5 cm , AE= 6 cm, BC= 12 cm and AB = 15 cm. Determine AC and DE.
 View Solution
View SolutionIn the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE
View SolutionConstruct a ΔABC in which AB = 5 cm, AC = 4.5 cm and ∠A=60∘.
View SolutionConstruct a ΔABC in which AB = 6.3 cm, AC = 4.5 cm and ∠A=45∘.
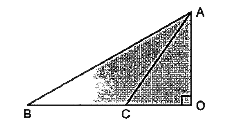
View SolutionIn triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
 View Solution
View SolutionIn the given figure, AB and DE are perpendiculars to BC. If AB = 9 cm, DE = 3 cm and AC = 24 cm, calculate AD.
 View Solution
View Solution

