Area of quadrilateral ABCD =Area of ΔABC+ area of _______
To solve the question, we need to express the area of quadrilateral ABCD in terms of the areas of triangles formed within it.
1. Identify the Quadrilateral: We have a quadrilateral ABCD.
2. Divide the Quadrilateral: We can divide quadrilateral ABCD into two triangles by drawing a diagonal. Let's draw diagonal AC. This gives us two triangles: Triangle ABC and Triangle ACD.
3. Area of Quadrilateral: The area of quadrilateral ABCD can be expressed as the sum of the areas of these two triangles:
Area of Quadrilateral ABCD=Area of Triangle ABC+Area of Triangle ACD
4. Expressing the Area: From the above expression, we can say:
Area of Quadrilateral ABCD=Area of Triangle ABC+Area of Triangle ACD
5. Final Expression: Therefore, the area of quadrilateral ABCD is equal to the area of triangle ABC plus the area of triangle ACD.
Conclusion:
The area of quadrilateral ABCD can be expressed as:
Area of Quadrilateral ABCD=Area of Triangle ABC+Area of Triangle ACD
Area of Quadrilateral ABCD=Area of Triangle ABC+Area of Triangle ACD
Area of Quadrilateral ABCD=Area of Triangle ABC+Area of Triangle ACD
The area of quadrilateral ABCD can be expressed as:
Area of Quadrilateral ABCD=Area of Triangle ABC+Area of Triangle ACD
Topper's Solved these Questions
- CBSE BOARDS 2020BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - CBSE BOARDS 2020EXERCISE - SECTION B
22 Videos
- CBSE BOARDS 2020BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - CBSE BOARDS 2020EXERCISE - SECTION C
33 Videos
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION-C
5 Videos
Similar Questions
G is the centroid of triangle ABC and A1 and B1 are the midpoints of sides AB and AC, respectively. If Δ1 is the area of quadrilateral GA1AB1 and Δ is the area of triangle ABC, then ΔΔ1 is equal to
View SolutionG is the centroid of triangle ABC and A1 and B1 are the midpoints of sides AB and AC, respectively. If Δ1 is the area of quadrilateral GA1AB1 and Δ is the area of triangle ABC, then ΔΔ1 is equal to
View Solution
Knowledge Check
In the figure, ABCD is a rectangle, and the area of quadrilateral AFCE is equal to the area of ΔABC. What is the value of x?
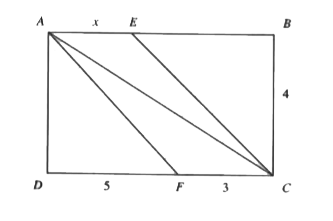 A5B6C7D12
A5B6C7D12In the figure, the area of the quadrilateral ABCD is 75. What is the area of parallelogram EFGH?
 A96B153C157D171
A96B153C157D171In the figure, ABCD and ABEF are parallelograms. The area of the quadrilateral ABED is 6. what is the area of the parallelogram ABCD?
 A2B4C4.5D5
A2B4C4.5D5
O' is an interior point of a parallelogram ABCD. Prove that :
area of ΔAOB+ area of ΔCOD= area of ΔAOD+ area of ΔBOC
View SolutionIn the given figure , DE //BC and
AD : AB= 2 : 5 Find :
area of ΔADE area of ΔABC
( ii) area of ΔABC area of trapezium DBCE

View SolutionIn the adjoning figure, D and E are the points on the sides AB and AC respectively of ΔABC and area of ΔBCE= area of ΔBCD.
Prove that DE∣∣BC

View Solution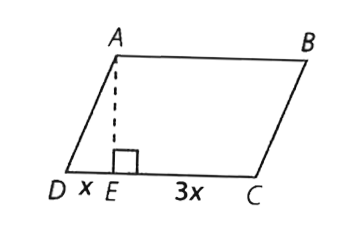
ABCD is parallelogram (see figure above) . The ratio of DE to EC is 1:3. Height AE has a length of 3. If quadrilateral ABCE has an area of 21, what is the area of ABCD?
View SolutionIn the figure, ABCD is a rectangle. The area of quadrilateral EBFD is one half the area of the rectangle ABCD. Which one of the following is the value of AD ?
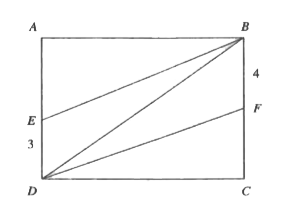
View Solution
