Let O be the circumcenter, H be the orthocentre, I be the incenter, and I1,I2,I3 be the excenters of acute-angled ABC. Column I Column II Angle subtended by OI at vertex A p. |B−C| Angle subtended by HI at vertex A q. ∣∣∣B−C2∣∣∣ Angle subtended by OH at vertex A r. B+C2 Angle subtended by I2I3atI1 A q. B2−C
To solve the problem, we need to analyze the angles subtended by the points O (circumcenter), H (orthocenter), I (incenter), and the excenters I1,I2,I3 at vertex A of triangle ABC.
1. Understanding the Geometry:
- We have a triangle ABC with its circumcenter O, orthocenter H, incenter I, and excenters I1,I2,I3.
- We need to find the angles subtended by the segments OI, HI, OH, and I2I3 at vertex A.
2. Angle Subtended by OI at Vertex A:
- The angle subtended by the line segment OI at vertex A can be expressed as p=|B−C|.
- This is based on the property that the angle subtended by the circumcenter and incenter at a vertex is related to the angles at the other vertices.
3. Angle Subtended by HI at Vertex A:
- The angle subtended by the line segment HI at vertex A can be expressed as q=∣∣∣B−C2∣∣∣.
- This follows from the relationship between the orthocenter, incenter, and the angles of the triangle.
4. Angle Subtended by OH at Vertex A:
- The angle subtended by the line segment OH at vertex A can be expressed as r=B+C2.
- This is derived from the fact that the circumcenter and orthocenter are related to the angles of the triangle.
5. Angle Subtended by I2I3 at I1:
- The angle subtended by the line segment I2I3 at I1 can be expressed as s=B2−C.
- This is based on the properties of the excenters and their relation to the angles of the triangle.
Summary of Results:
- The angles subtended at vertex A are:
- OI subtends angle p=|B−C|
- HI subtends angle q=∣∣∣B−C2∣∣∣
- OH subtends angle r=B+C2
- I2I3 subtends angle s=B2−C
- We have a triangle ABC with its circumcenter O, orthocenter H, incenter I, and excenters I1,I2,I3.
- We need to find the angles subtended by the segments OI, HI, OH, and I2I3 at vertex A.
- The angle subtended by the line segment OI at vertex A can be expressed as p=|B−C|.
- This is based on the property that the angle subtended by the circumcenter and incenter at a vertex is related to the angles at the other vertices.
- The angle subtended by the line segment HI at vertex A can be expressed as q=∣∣∣B−C2∣∣∣.
- This follows from the relationship between the orthocenter, incenter, and the angles of the triangle.
- The angle subtended by the line segment OH at vertex A can be expressed as r=B+C2.
- This is derived from the fact that the circumcenter and orthocenter are related to the angles of the triangle.
- The angle subtended by the line segment I2I3 at I1 can be expressed as s=B2−C.
- This is based on the properties of the excenters and their relation to the angles of the triangle.
- The angles subtended at vertex A are:
- OI subtends angle p=|B−C|
- HI subtends angle q=∣∣∣B−C2∣∣∣
- OH subtends angle r=B+C2
- I2I3 subtends angle s=B2−C
Topper's Solved these Questions
Similar Questions
If I1,I2,I3 are the centers of escribed circles of triangle ABC, show that area of triangle I1I2I3=abc2r.
View SolutionIf the chord y=mx+c subtends a right angle at the vertex of the parabola y2=4ax, thenthe value of c is
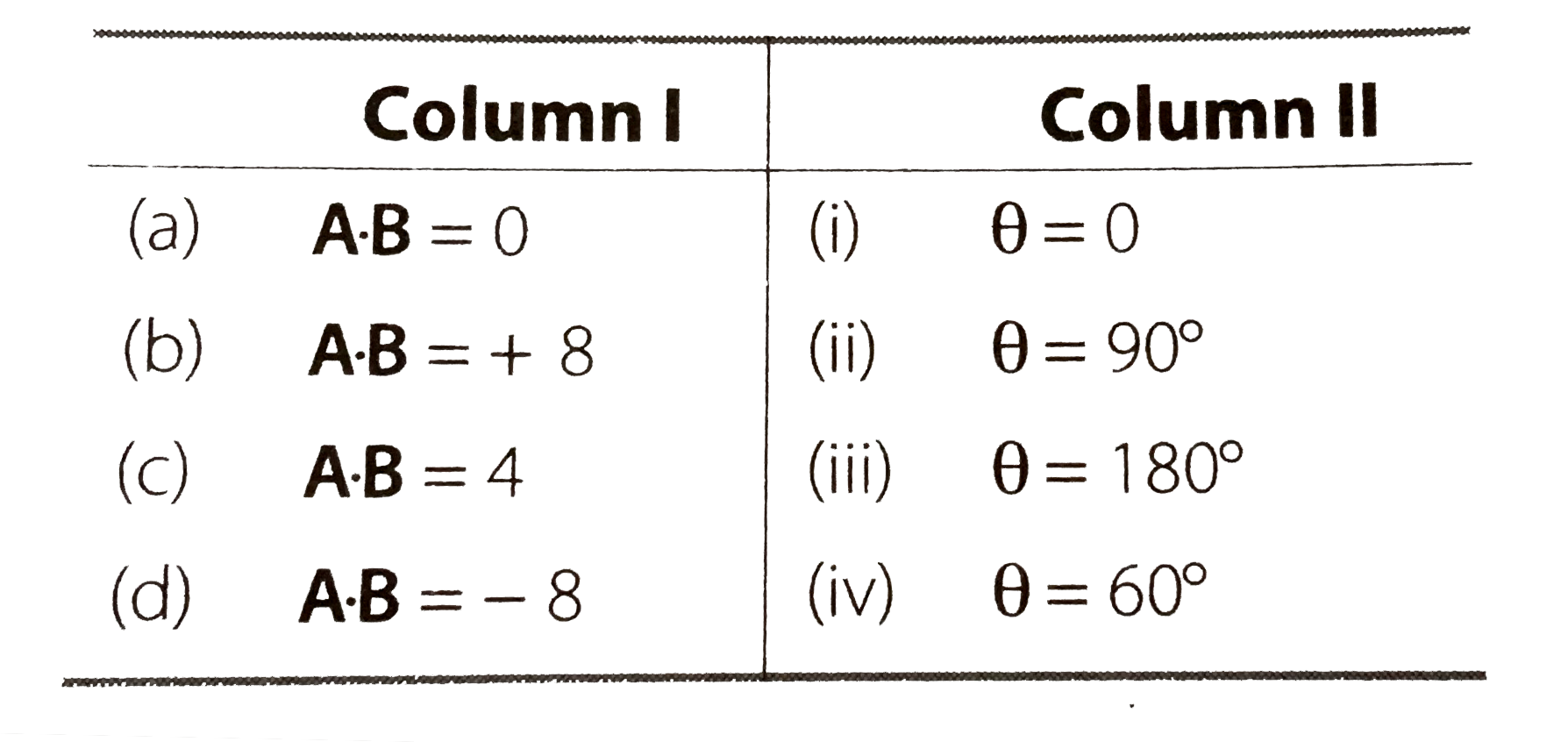
View SolutionIf |A|=2 and |B| = 4, then match the relation in Column I with the angle θ between A and B in Column II.
View SolutionIn a circle of radius 21 cm, an arc subtends an angle of 60o at the centre. Find: (i) length of the arc
View SolutionIf I is the incenter of ABCandR1,R2,andR3 re, respectively, the radii of the circumcircles of the triangles IBC,ICAandIAB, then prove that R1R2R3=2rR2.
View SolutionFind the eccentricity of the ellipse of minor axis 2b, if the line segment joining the foci subtend and angle 2θ at the upper vertex.
View SolutionDetermine the currents I1,I2,andI3 for the network shown below
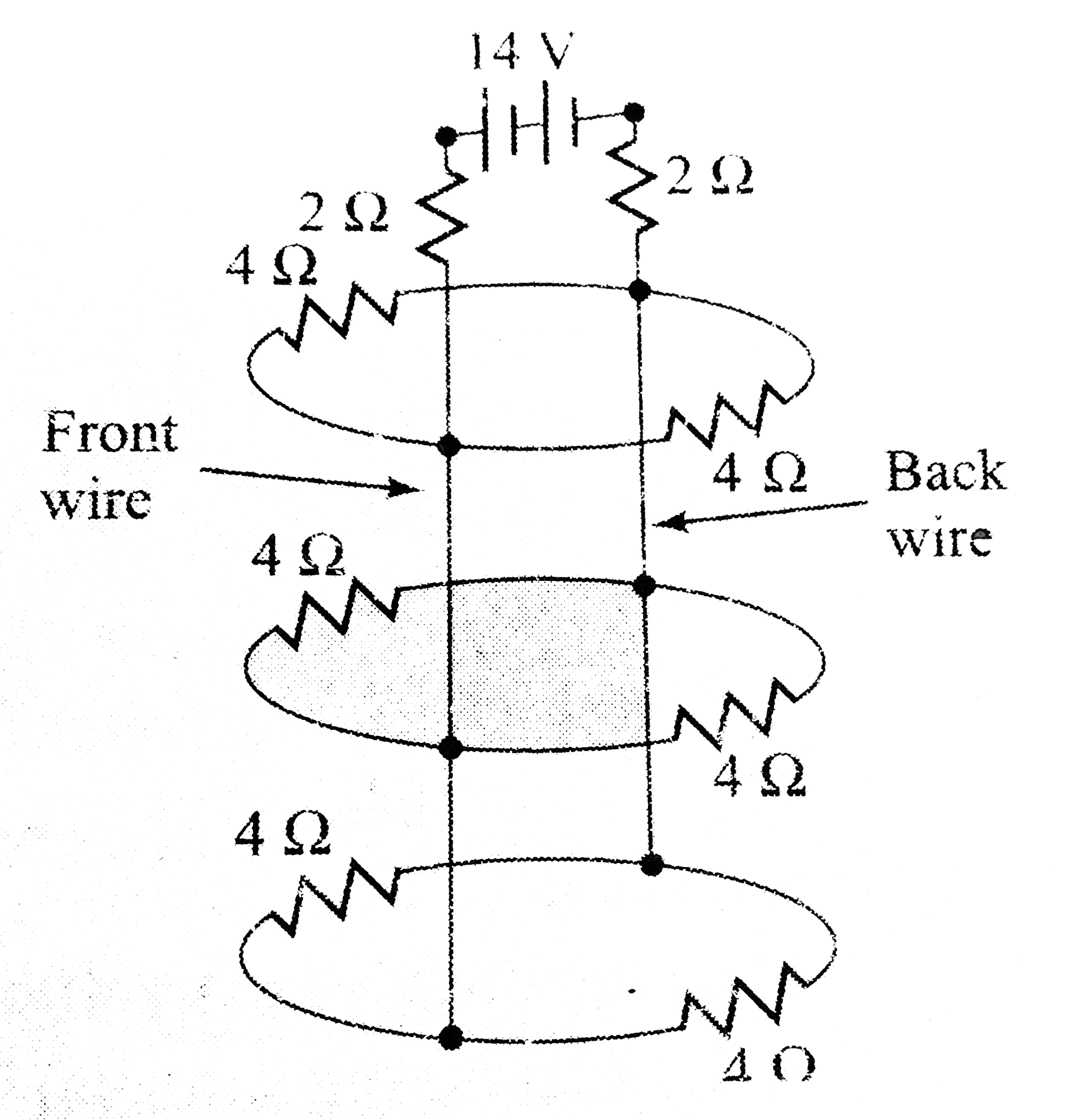
a. I1=……….,b.I2=………….,c.I3=…………….
View SolutionWhich of these statements is not true ?
(a) Point A and B lie in the interior of the angle
(b) Points C and D lie in the exterior of the angle.
( c )Point P is the vertex of the angle .
(d) Point R is the vertex of the angle.

View SolutionIf B is an idempotent matrix, and A=I−B, then a. A2=A b. A2=I c. AB=O d. BA=O
View SolutionThe angle subtended by the double ordinate of length 8a of the parabola y2=4ax at its vertex is a) π3 b) π4 c) π2 d) π6
View Solution
