Each side of triangle ABC is divided into three equal parts. Find the ratio of the area of hexagon PQRSTU to the area of the triangle ABC.
To find the ratio of the area of hexagon PQRSTU to the area of triangle ABC, we will follow these steps:
Step 1: Understand the Division of Triangle Sides
Each side of triangle ABC is divided into three equal parts. Let the lengths of the sides be:
- AB=c
- BC=a
- CA=b
Thus, each segment on the sides will be:
- c3, c3, c3 for side AB
- a3, a3, a3 for side BC
- b3, b3, b3 for side CA
Step 2: Identify the Hexagon
The hexagon PQRSTU is formed by removing three small triangles from the corners of triangle ABC. The vertices of the hexagon are the points where the segments intersect.
Step 3: Calculate the Area of Triangle ABC
The area Δ of triangle ABC can be calculated using the formula:
Δ=12×base×height
Alternatively, using the sides and the sine of the included angle:
Δ=12×b×c×sinA
Step 4: Calculate the Area of the Small Triangles
The area of each small triangle removed from the corners can be calculated as follows:
1. For triangle APQ:
AreaAPQ=12×c3×b3×sinA=cbsinA18
2. For triangle BUT:
AreaBUT=12×c3×a3×sinB=casinB18
3. For triangle RSC:
AreaRSC=12×a3×b3×sinC=absinC18
Step 5: Total Area of the Small Triangles
The total area of the three triangles is:
Total Areatriangles=cbsinA18+casinB18+absinC18
This can be factored as:
Total Areatriangles=118(cbsinA+casinB+absinC)
Step 6: Area of Hexagon PQRSTU
The area of hexagon PQRSTU can be found by subtracting the total area of the small triangles from the area of triangle ABC:
Areahexagon=Δ−Total Areatriangles
Substituting the values:
Areahexagon=Δ−118(cbsinA+casinB+absinC)
Step 7: Ratio of Areas
To find the ratio of the area of hexagon PQRSTU to the area of triangle ABC:
Ratio=AreahexagonΔ
Substituting the values:
Ratio=Δ−118(cbsinA+casinB+absinC)Δ
This simplifies to:
Ratio=1−118⋅(cbsinA+casinB+absinC)Δ
Given that the total area of the triangles removed is 13Δ, we find:
Ratio=23
Final Answer
The ratio of the area of hexagon PQRSTU to the area of triangle ABC is 23.
---
Each side of triangle ABC is divided into three equal parts. Let the lengths of the sides be:
- AB=c
- BC=a
- CA=b
- c3, c3, c3 for side AB
- a3, a3, a3 for side BC
- b3, b3, b3 for side CA
The hexagon PQRSTU is formed by removing three small triangles from the corners of triangle ABC. The vertices of the hexagon are the points where the segments intersect.
The area Δ of triangle ABC can be calculated using the formula:
Δ=12×base×height
Alternatively, using the sides and the sine of the included angle:
Δ=12×b×c×sinA
The area of each small triangle removed from the corners can be calculated as follows:
1. For triangle APQ:
AreaAPQ=12×c3×b3×sinA=cbsinA18
2. For triangle BUT:
AreaBUT=12×c3×a3×sinB=casinB18
3. For triangle RSC:
AreaRSC=12×a3×b3×sinC=absinC18
The total area of the three triangles is:
Total Areatriangles=cbsinA18+casinB18+absinC18
This can be factored as:
Total Areatriangles=118(cbsinA+casinB+absinC)
The area of hexagon PQRSTU can be found by subtracting the total area of the small triangles from the area of triangle ABC:
Areahexagon=Δ−Total Areatriangles
Substituting the values:
Areahexagon=Δ−118(cbsinA+casinB+absinC)
To find the ratio of the area of hexagon PQRSTU to the area of triangle ABC:
Ratio=AreahexagonΔ
Substituting the values:
Ratio=Δ−118(cbsinA+casinB+absinC)Δ
This simplifies to:
Ratio=1−118⋅(cbsinA+casinB+absinC)Δ
Given that the total area of the triangles removed is 13Δ, we find:
Ratio=23
The ratio of the area of hexagon PQRSTU to the area of triangle ABC is 23.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. Find the ratio of the area of Δ ABC to the area of the parallelogram ABCD.
View SolutionP is a point inside the triangle ABC. Lines are drawn through P, parallel to the sides of the triangle.The three resulting triangles with the vertex at P have areas 4,9and49sq. units. The area of the triangle ABC is -
View Solution
Knowledge Check
In the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2In the figure, what is the area of ΔABC?
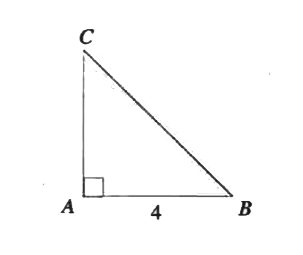 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information givenIf the area of △ABC is 21, and the length of the height minus the length of the base equals 1, which of the following is equal to the base of the triangle ?
A2B4C6D7
Sides of triangle ABC, a, b, c are in G.P. If 'r' be the common ratio of this G.P. , then
View SolutionIn the given figure, ABC is a right angled triangle with ∠BAC=90∘.

Find the ratio of the area of DetlaADB is to area of ΔCDA.
View SolutionIn a triangle ABC, prove that the ratio of the area of the incircle to that of the triangle is π:cot(A2)cot(B2)cot(C2)
View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.
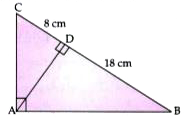
Find the ratio of the area of ΔADB to area of ΔCDA.
View SolutionAn equilateral triangle and a regular hexagon has same perimeter. Find the ratio of their areas.
View Solution