Match the statement/expressions in Column I with the statements/expressions in Column II. Column I Column II The minimum value of x2+2x+4x+2 is (p) 0 Let AandBbe3x3 matrices of real numbers, where A is symmetric, B is skew symmetric, and (A+B)(A−B)=(A−B)(A+B) if (AB)t=(−1)kAB, where (AB)t is the transpose of the matrix AB , then the possible values of k are (q) 1 Let a=(log)3(log)32. An integer k satisfying 1<2−k+3(−1)<2, must be less than (r) 2 In sinθ=cosφ, then the possible values of 1π(θ±φ−π2) are (s) 3
To match the statements in Column I with those in Column II, we will analyze each expression step by step.
Step 1: Analyze the first statement
Statement: The minimum value of (x2+2x+4)/(x+2)
To find the minimum value, we can rewrite the expression:
y=x2+2x+4x+2
We can simplify this by performing polynomial long division or by substituting x+2=t (where t=x+2, hence x=t−2):
y=(t−2)2+2(t−2)+4t=t2−4t+4+2t−4+4t=t2−2t+4t
This simplifies to:
y=t−2+4t
To find the minimum, we can take the derivative and set it to zero:
dydt=1−4t2
Setting the derivative to zero:
1−4t2=0⟹t2=4⟹t=2
Substituting t=2 back into the expression for y:
y=2−2+42=2
Thus, the minimum value is 2.
Step 2: Analyze the second statement
Statement: Let A and B be 3×3 matrices of real numbers, where A is symmetric, B is skew-symmetric, and (A+B)(A−B)=(A−B)(A+B).
Using the property of symmetric and skew-symmetric matrices, we know that:
AT=AandBT=−B
From the equation (A+B)(A−B)=(A−B)(A+B), we can expand both sides and simplify. After simplification, we find that AB=BA.
Given that (AB)T=(−1)kAB, we can deduce that k must be odd because the transpose of a product of matrices reverses the order and changes the sign of skew-symmetric matrices.
Thus, the possible values of k are 1.
Step 3: Analyze the third statement
Statement: Let a=log3(log32). An integer k satisfying 1<2−k+3−1<2.
Rearranging the inequality:
1<2−k+13<2
Taking logarithm base 2:
0<−k+13<1
This gives us two inequalities:
1. −k+13>0⟹k<13
2. −k+13<1⟹k>−23
Since k must be an integer, the only integer satisfying this is k<0. The maximum integer k can be is −1.
Thus, k must be less than 2.
Step 4: Analyze the fourth statement
Statement: In sinθ=cosφ, the possible values of 1π(θ±φ−π2).
Using the identity sinθ=cosφ, we can write:
θ=π2−φ+nπ(n∈Z)
Thus,
1π(θ±φ−π2)=1π(±φ+nπ)=n±φπ
The possible values of n can be any integer, hence the total number of distinct values is 3.
Final Matching
Now we can match the statements:
- The minimum value of (x2+2x+4)/(x+2) is 2 (matches with r).
- Possible values of k are 1 (matches with q).
- k must be less than 2 (matches with r).
- The possible values of 1π(θ±φ−π2) are 3 (matches with s).
Final Matches
- (r) 2
- (q) 1
- (s) 3
Statement: The minimum value of (x2+2x+4)/(x+2)
Statement: Let A and B be 3×3 matrices of real numbers, where A is symmetric, B is skew-symmetric, and (A+B)(A−B)=(A−B)(A+B).
Statement: Let a=log3(log32). An integer k satisfying 1<2−k+3−1<2.
2. −k+13<1⟹k>−23
Statement: In sinθ=cosφ, the possible values of 1π(θ±φ−π2).
Now we can match the statements:
- Possible values of k are 1 (matches with q).
- k must be less than 2 (matches with r).
- The possible values of 1π(θ±φ−π2) are 3 (matches with s).
- (r) 2
- (q) 1
- (s) 3
Topper's Solved these Questions
Similar Questions
Let AandB be 3×3 matrtices of real numbers, where A is symmetric, B is skew-symmetric , and (A+B)(A−B)=(A−B)(A+B). If (AB)t=(−1)kAB,where.(AB)t is the transpose of the mattix AB, then find the possible values of k.
View SolutionIf |A|=2 and |B| = 4, then match the relation in Column I with the angle θ between A and B in Column II.
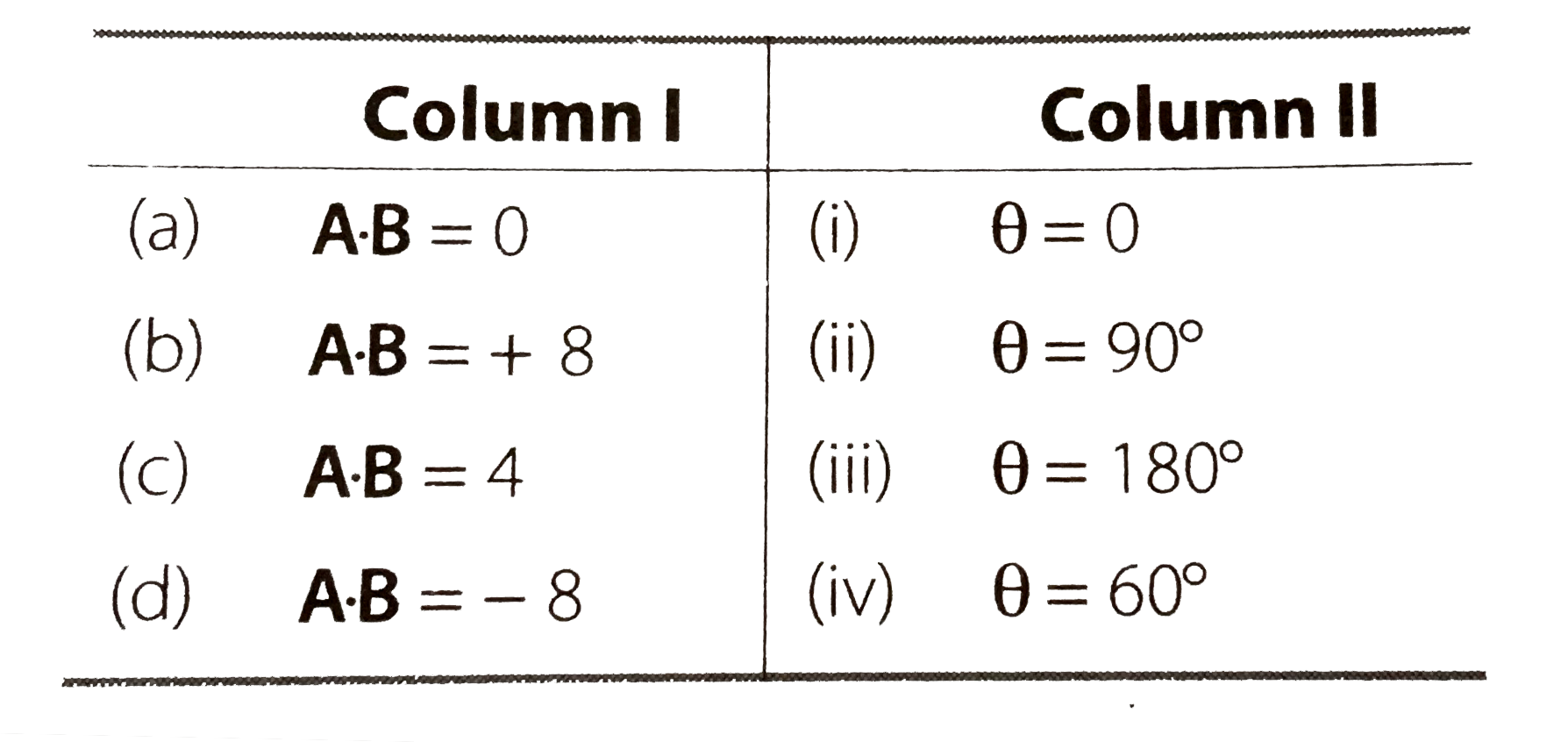
View Solution
Knowledge Check
Match the Column I and Column II.,B
 AA-p, B-q, C-r, D-sBA-q, B-r, C-s. D-pCA-r, B-q, C-p, D-pDA-r, B-s, C-p, D-q
AA-p, B-q, C-r, D-sBA-q, B-r, C-s. D-pCA-r, B-q, C-p, D-pDA-r, B-s, C-p, D-q
Let a,b,c be positive real numbers with abc=1 let A =⎡⎢⎣abcbcacab⎤⎥⎦ifATA=I where AT is the transpose of A and I is the identity matrix , then determine the value of a2+b2+c2
View SolutionIf A=[1203] is written as B+C , where B is a symmetric matrix and C is a skew-symmetric matrix, then find B.
View SolutionIf A is a symmetric matrix and B is a skew-symmetric matrix such that
A+B=[235−1], then AB is equal to
View SolutionIf A is a symmetric matrix and B is a skew-symmetric matrix such that
A+B=[235−1], then AB is equal to
View SolutionIf A and B are symmetric matrices of order n(A≠B) then (A) A+B is skew symmetric (B) A+B is symmetric (C) A+B is a diagonal matrix (D) A+B is a zero matrix
View SolutionIf A and B are symmetric matrices, then ABA is (a) symmetric matrix (b) skew-symmetric matrix (c) diagonal matrix (d) scalar matrix
View SolutionExpress the matrix B=[2−2−13] as the sum of a symmetric and a skew symmetric matrix.
View Solution
